Giải chuyên đề Tin 12 Cánh diều Bài 2: Biểu diễn đồ thị trên máy tính có đáp án

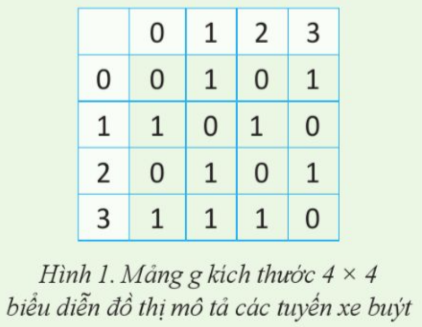
Nam thu thập thông tin về tuyến xe buýt giữa các địa điểm và kí hiệu như trong Bảng 1. Ví dụ, trên hàng bắt đầu bằng kí tự A cho biết từ địa điểm A có hai tuyến xe buýt, tuyến thứ nhất từ A tới B và tuyến thứ hai từ A tới D. Dựa trên mô tả của bảng thông tin về các tuyến xe buýt, chúng ta có thể trả lời các câu hỏi như sau:

- Từ D đến các địa điểm khác: 4 tuyến xe buýt

- Từ B đến D: có 1 tuyến xe buýt

* Nếu coi các địa điểm A, B, C, D trong Bảng 1 tương ứng là các đỉnh 0, 1, 2, 3 của đồ thị thì mảng hai chiều g trong Hình 1 biểu diễn đồ thị mô tả tuyến xe buýt giữa các địa điểm. 

Nếu Nam bổ sung thêm thông tin có một tuyến xe buýt từ B đến D, thì mảng g biểu diễn đồ thị thay đổi như sau: Vì B và D tương ứng với đỉnh 1 và 3, bạn sẽ thêm số ‘1’ vào vị trí (1,3) và (3,1) trong ma trận để biểu diễn tuyến đường trực tiếp giữa hai địa điểm này.

* Nhận xét tính đối xứng của mảng:

- Cập nhật ma trận: Ma trận này sau khi thêm tuyến đường mới sẽ trông như sau:

- Tính đối xứng: Tất cả các tuyến xe buýt đều là hai chiều vì ma trận có tính đối xứng qua đường chéo chính, nghĩa là nếu có tuyến đường từ đỉnh i đến đỉnh j được biểu diễn bằng số ‘1’ tại vị trí (i,j), thì cũng có tuyến đường từ đỉnh j về đỉnh i được biểu diễn bằng số ‘1’ tại vị trí (j,i).

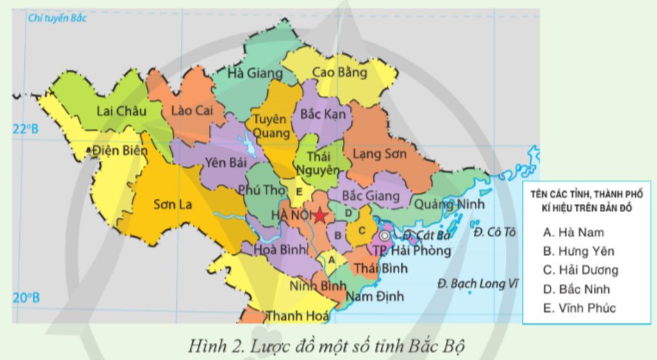
Xây dựng mảng g biểu diễn đồ thị cho mối quan hệ giáp ranh giữa 8 tỉnh (các tỉnh được đánh số từ 0 đến 7): Sơn La (0), Điện Biên (1), Lai Châu (2), Lào Cai (3), Hà Giang (4), Cao Bằng (5), Lạng Sơn (6), Quảng Ninh (7) như sau: Để xây dựng mảng g biểu diễn đồ thị cho mối quan hệ giáp ranh giữa 8 tỉnh, bạn sẽ cần tạo một ma trận vuông kích thước 8x8, với mỗi hàng và cột tương ứng với một tỉnh từ 0 đến 7. Nếu tỉnh ‘i’ giáp ranh với tỉnh ‘j’, ô tại hàng ‘i’ và cột ‘j’ sẽ được đánh dấu là 1; nếu không, sẽ là 0.

Về số lượng số 0 và số 1 trong mảng g:

- Số lượng số 0: Sẽ có nhiều số 0 hơn vì không phải tỉnh nào cũng giáp ranh với tất cả các tỉnh khác.

- Số lượng số 1: Số lượng số 1 sẽ ít hơn vì chỉ có các tỉnh giáp ranh mới được kết nối với nhau.

Ma trận g sẽ có tính đối xứng qua đường chéo chính, phản ánh mối quan hệ giáp ranh hai chiều giữa các tỉnh. Điều này cũng cho thấy rằng đồ thị là không hướng, biểu diễn mối quan hệ không phân biệt hướng giữa các tỉnh.

Một đồ thị gồm 4 đỉnh, các đỉnh được đánh số từ 0 đến 3, được biểu diễn bằng ma trận kề như Hình 3. Ma trận kề cho thấy từ đỉnh 1 đến được đỉnh 0 và đỉnh 2. 

a) Đỉnh đến được đỉnh 2: là đỉnh 0 và đỉnh 1.

b) Biểu diễn đồ thị bằng danh sách kề:

- Đỉnh 0 kề với đỉnh [1, 2]

- Đỉnh 1 kề với đỉnh [0]

- Đỉnh 2 kề với đỉnh [0]

- Đỉnh 3 không kề với đỉnh nào

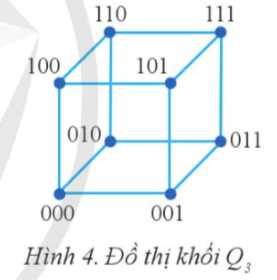
Đồ thị khối Q, (Hình 4) là đồ thị có 8 đỉnh, mỗi đỉnh là một dãy bit độ dài 3, hai đinh có cạnh nối nếu hai dãy bit sai khác nhau đúng một bit. 

- Biểu diễn đồ thị bằng Ma trận kề: Ma trận kề sẽ có kích thước 8x8, với mỗi hàng và cột tương ứng với một đỉnh của đồ thị. Nếu hai đỉnh khác nhau đúng một bit, chúng sẽ được nối với nhau và ô tương ứng trong ma trận sẽ được đánh dấu là 1. Còn lại sẽ là 0.

a) Sai. Vì cả đơn đồ thị vô hướng và đơn đồ thị có hướng đều có thể biểu diễn được bằng ma trận kề.

b) Đúng. Vì cách biểu diễn đồ thị bằng ma trận kề tuy đơn giản nhưng có thể lãng phí bộ nhớ trong trường hợp đồ thị có nhiều đỉnh nhưng có ít cạnh. Lý do là vì ma trận kề là một ma trận vuông có kích thước n x n, trong đó n là số đỉnh của đồ thị.

c) Sai.Vì cả đơn đồ thị vô hướng và đơn đồ thị có hướng đều có thể biểu diễn được bằng danh sách kề.

d) Đúng. Vì cách biểu diễn bằng danh sách kề sẽ phù hợp khi đồ thị có nhiều đỉnh nhưng có ít cạnh. Lý do là vì danh sách kề chỉ lưu trữ thông tin về các cạnh thực sự tồn tại trong đồ thị, do đó sẽ tiết kiệm bộ nhớ hơn so với ma trận kề, đặc biệt là khi đồ thị có nhiều đỉnh nhưng có ít cạnh.