Nếu coi các địa điểm A, B, C, D trong Bảng 1 tương ứng là các đỉnh 0, 1, 2, 3 của đồ thị thì mảng hai chiều g trong Hình 1 biểu diễn đồ thị mô tả tuyến xe buýt giữa các địa điểm.

Nếu Nam bổ sung thêm thông tin có một tuyến xe buýt từ B đến D, thì mảng g biểu diễn đồ thị thay đổi như thế nào?

Em có nhận xét gì về tính đối xứng của mảng ?

Xem lời giải

Câu hỏi trong đề: Giải chuyên đề Tin 12 Cánh diều Bài 2: Biểu diễn đồ thị trên máy tính có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

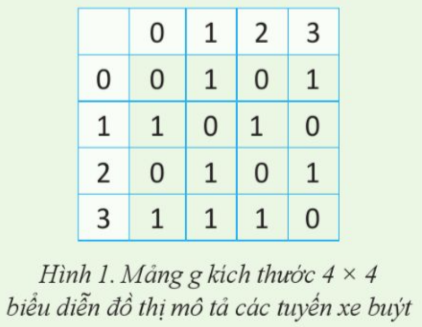
* Nếu coi các địa điểm A, B, C, D trong Bảng 1 tương ứng là các đỉnh 0, 1, 2, 3 của đồ thị thì mảng hai chiều g trong Hình 1 biểu diễn đồ thị mô tả tuyến xe buýt giữa các địa điểm.

Nếu Nam bổ sung thêm thông tin có một tuyến xe buýt từ B đến D, thì mảng g biểu diễn đồ thị thay đổi như sau: Vì B và D tương ứng với đỉnh 1 và 3, bạn sẽ thêm số ‘1’ vào vị trí (1,3) và (3,1) trong ma trận để biểu diễn tuyến đường trực tiếp giữa hai địa điểm này.

* Nhận xét tính đối xứng của mảng:

- Cập nhật ma trận: Ma trận này sau khi thêm tuyến đường mới sẽ trông như sau:

Nếu coi các địa điểm A, B, C, D trong Bảng 1 tương ứng là các đỉnh 0, 1, 2, 3 của đồ thị thì mảng hai chiều g trong Hình 1 biểu diễn đồ thị mô tả tuyến xe buýt giữa các địa điểm. (ảnh 2)

- Tính đối xứng: Tất cả các tuyến xe buýt đều là hai chiều vì ma trận có tính đối xứng qua đường chéo chính, nghĩa là nếu có tuyến đường từ đỉnh i đến đỉnh j được biểu diễn bằng số ‘1’ tại vị trí (i,j), thì cũng có tuyến đường từ đỉnh j về đỉnh i được biểu diễn bằng số ‘1’ tại vị trí (j,i).

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Đồ thị khối Q, (Hình 4) là đồ thị có 8 đỉnh, mỗi đỉnh là một dãy bit độ dài 3, hai đinh có cạnh nối nếu hai dãy bit sai khác nhau đúng một bit.

Em hãy biểu diễn đồ thị bằng ma trận kề và danh sách kề.

Xem đáp án

Lời giải

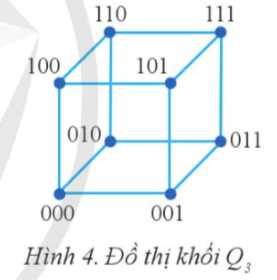
Đồ thị khối Q, (Hình 4) là đồ thị có 8 đỉnh, mỗi đỉnh là một dãy bit độ dài 3, hai đinh có cạnh nối nếu hai dãy bit sai khác nhau đúng một bit.

- Biểu diễn đồ thị bằng Ma trận kề: Ma trận kề sẽ có kích thước 8x8, với mỗi hàng và cột tương ứng với một đỉnh của đồ thị. Nếu hai đỉnh khác nhau đúng một bit, chúng sẽ được nối với nhau và ô tương ứng trong ma trận sẽ được đánh dấu là 1. Còn lại sẽ là 0.

Đồ thị khối Q, (Hình 4) là đồ thị có 8 đỉnh, mỗi đỉnh là một dãy bit độ dài 3, hai đinh có cạnh nối nếu hai dãy bit sai khác nhau đúng một bit. Em hãy biểu diễn đồ thị bằng ma trận kề và danh sách kề. (ảnh 2)

- Biểu diễn đồ thị bằng Danh sách kề: Danh sách kề sẽ liệt kê các đỉnh kề với mỗi đỉnh trong đồ thị.

Câu 2

Một đồ thị gồm 4 đỉnh, các đỉnh được đánh số từ 0 đến 3, được biểu diễn bằng ma trận kề như Hình 3. Ma trận kề cho thấy từ đỉnh 1 đến được đỉnh 0 và đỉnh 2.

a) Em hãy cho biết những đỉnh nào đến được đỉnh 2.

b) Em hãy biểu diễn đồ thị bằng danh sách kề.

Xem đáp án

Lời giải

Một đồ thị gồm 4 đỉnh, các đỉnh được đánh số từ 0 đến 3, được biểu diễn bằng ma trận kề như Hình 3. Ma trận kề cho thấy từ đỉnh 1 đến được đỉnh 0 và đỉnh 2.

a) Đỉnh đến được đỉnh 2: là đỉnh 0 và đỉnh 1.

b) Biểu diễn đồ thị bằng danh sách kề:

- Đỉnh 0 kề với đỉnh [1, 2]

- Đỉnh 1 kề với đỉnh [0]

- Đỉnh 2 kề với đỉnh [0]

- Đỉnh 3 không kề với đỉnh nào

Câu 3