Câu hỏi:
17/09/2024 502
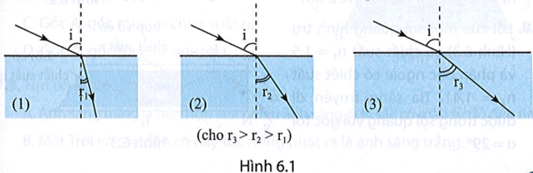
Ba môi trường trong suốt là không khí và hai môi trường khác có các chiết suất tuyệt đối n1, n2 (với n2 > n1). Lần lượt cho ánh sáng truyền đến mặt phân cách của tất cả các cặp môi trường có thể tạo ra. Biểu thức nào sau đây không thể là sin của góc tới hạn ith đối với cặp môi trường tương ứng?
A.
B.
C.
D.
Ba môi trường trong suốt là không khí và hai môi trường khác có các chiết suất tuyệt đối n1, n2 (với n2 > n1). Lần lượt cho ánh sáng truyền đến mặt phân cách của tất cả các cặp môi trường có thể tạo ra. Biểu thức nào sau đây không thể là sin của góc tới hạn ith đối với cặp môi trường tương ứng?
A.
B.
C.
D.
Câu hỏi trong đề:
Giải SBT KHTN 9 KNTT Bài 6. Phản xạ toàn phần !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: A
Trong bài toán này, chúng ta có 3 môi trường: không khí (giả sử chiết suất gần bằng 1), môi trường 1 (chiết suất n1) và môi trường 2 (chiết suất n2 với n2 > n1). Có 3 cặp môi trường có thể tạo ra:
- Không khí - môi trường 1: Ánh sáng truyền từ không khí (chiết suất nhỏ hơn) sang môi trường 1 (chiết suất lớn hơn). Trong trường hợp này, sẽ không có góc tới hạn. Bởi vì ánh sáng luôn bị khúc xạ khi truyền từ môi trường chiết suất nhỏ sang môi trường chiết suất lớn.
- Không khí - môi trường 2: Tương tự như trường hợp 1, sẽ không có góc tới hạn.
- Môi trường 1 - môi trường 2: Ánh sáng truyền từ môi trường 1 (chiết suất nhỏ hơn) sang môi trường 2 (chiết suất lớn hơn). Trong trường hợp này, sẽ có góc tới hạn.
Công thức tính góc tới hạn: .
Vậy biểu thức không thể là sin của góc tới hạn ith đối với cặp môi trường tương ứng.
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Tia sáng truyền từ không khí vào chất lỏng với góc tới i = 60° thì góc khúc xạ r = 30°. Khi chiếu tia sáng đó từ chất lỏng ra không khí, muốn có phản xạ toàn phần thì góc tới i phải thoả mãn điều kiện nào dưới đây? Cho biết sin 35,26°0,58.
A. i > 42°.
B. i < 42°.
C. i > 35,26°.
D. i > 28,5°.
Tia sáng truyền từ không khí vào chất lỏng với góc tới i = 60° thì góc khúc xạ r = 30°. Khi chiếu tia sáng đó từ chất lỏng ra không khí, muốn có phản xạ toàn phần thì góc tới i phải thoả mãn điều kiện nào dưới đây? Cho biết sin 35,26°0,58.
A. i > 42°.
B. i < 42°.
C. i > 35,26°.
D. i > 28,5°.
Xem đáp án »
17/09/2024
3,886
Câu 2:
Khi ánh sáng truyền từ môi trường có chiết suất n, tới môi trường có chiết suất n2 thì điều kiện để xảy ra phản xạ toàn phần tại mặt phân cách giữa hai môi trường này là:
A. Chỉ cần n1 > n2.
B. Chỉ cần góc tới lớn hơn hoặc bằng góc tới hạn: iith.
C. n1 > n2 và góc tới lớn hơn hoặc bằng góc tới hạn: iith.
D. n1 > n2 và góc tới nhỏ hơn hoặc bằng góc tới hạn: i ith.
Khi ánh sáng truyền từ môi trường có chiết suất n, tới môi trường có chiết suất n2 thì điều kiện để xảy ra phản xạ toàn phần tại mặt phân cách giữa hai môi trường này là:
A. Chỉ cần n1 > n2.
B. Chỉ cần góc tới lớn hơn hoặc bằng góc tới hạn: iith.
C. n1 > n2 và góc tới lớn hơn hoặc bằng góc tới hạn: iith.
D. n1 > n2 và góc tới nhỏ hơn hoặc bằng góc tới hạn: i ith.
Xem đáp án »
17/09/2024
1,379
Câu 4:
Có tia sáng truyền từ không khí vào ba môi trường (1), (2), (3) như Hình 6.1.
Phản xạ toàn phần có thể xảy ra khi ánh sáng truyền trong cặp môi trường nào sau đây?
A. Từ (2) tới (1).
B. Từ (1) tới (2).
C. Từ (3) tới (1).
D. Từ (3) tới (2).
Có tia sáng truyền từ không khí vào ba môi trường (1), (2), (3) như Hình 6.1.
Phản xạ toàn phần có thể xảy ra khi ánh sáng truyền trong cặp môi trường nào sau đây?
A. Từ (2) tới (1).
B. Từ (1) tới (2).
C. Từ (3) tới (1).
D. Từ (3) tới (2).
Xem đáp án »
17/09/2024
736
Câu 5:
Ghép nội dung ở cột bên trái với nội dung tương ứng ở cột bên phải để có một phát biểu đúng và đầy đủ.
Ghép nội dung ở cột bên trái với nội dung tương ứng ở cột bên phải để có một phát biểu đúng và đầy đủ.
Xem đáp án »
17/09/2024
682
Câu 6:
Một khối thuỷ tinh có tiết diện thẳng như Hình 6.2 đặt trong không khí, ABCD là hình vuông, CDE là tam giác vuông cân. Trong mặt phẳng của tiết diện thẳng, chiếu một chùm tia sáng đơn sắc hẹp SI vuông góc với DE (IE < ID). Biết chiết suất của thuỷ tinh là n = 1,5. Vẽ đường đi của tia sáng trong khối thuỷ tinh. Phương của tia ló hợp với pháp tuyến của mặt mà tia sáng ló ra một góc bằng bao nhiêu độ?
Xem đáp án »
17/09/2024
584
Câu 7:
Một cái đinh được cắm vuông góc vào tâm O của một tấm gỗ hình tròn có bán kính R = 0,05 m. Tấm gỗ được thả nổi trên mặt thoáng của một chậu nước (Hình 6.4). Đầu A của đinh ở trong nước. Cho chiết suất của nước là .
a) Cho chiều dài OA của đinh ở trong nước là 8,7 cm. Hỏi đặt mắt ở trong không khí nhìn đầu đinh theo phương đi sát mép gỗ sẽ thấy đầu đinh ở cách mặt nước một khoảng bao nhiêu?
b) Cho chiều dài OA giảm dần. Xác định khoảng cách OA để mắt không còn nhìn thấy đầu A của đinh.
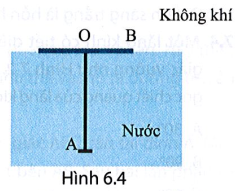
Một cái đinh được cắm vuông góc vào tâm O của một tấm gỗ hình tròn có bán kính R = 0,05 m. Tấm gỗ được thả nổi trên mặt thoáng của một chậu nước (Hình 6.4). Đầu A của đinh ở trong nước. Cho chiết suất của nước là .
a) Cho chiều dài OA của đinh ở trong nước là 8,7 cm. Hỏi đặt mắt ở trong không khí nhìn đầu đinh theo phương đi sát mép gỗ sẽ thấy đầu đinh ở cách mặt nước một khoảng bao nhiêu?
b) Cho chiều dài OA giảm dần. Xác định khoảng cách OA để mắt không còn nhìn thấy đầu A của đinh.
Xem đáp án »
18/09/2024
515
về câu hỏi!