Câu hỏi:
03/10/2024 3,185
a) Tìm các hệ số \(x\) và \(y\) trong phản ứng hóa học đã được cân bằng sau:
\(x{\rm{FeO}} + y{{\rm{O}}_2}\mathop \to \limits^{{\rm{t}}^\circ } 2{\rm{F}}{{\rm{e}}_3}{{\rm{O}}_4}.\)
Từ đó, hãy hoàn thiện phương trình phản ứng hóa học sau khi được cân bằng.
b) Giải bài toán sau bằng cách lập hệ phương trình:
Một đoàn khách du lịch gồm 40 người dự định tham quan chùa Hương (Hà Nội) bằng cáp treo khứ hồi (gồm lượt lên và lượt xuống). Nhưng khi tới nơi có 5 bạn trẻ muốn khám phá bằng đường bộ khi leo lên còn lúc xuống sẽ đi cáp treo để trải nghiệm nên 5 bạn chỉ mua vé lượt xuống, do đó đoàn đã chi ra \[8{\rm{ }}450{\rm{ }}000\] đồng để mua vé. Hỏi giá vé cáp treo khứ hồi và giá vé cáp treo 1 lượt là bao nhiêu? Biết rằng giá vé 1 lượt rẻ hơn giá vé khứ hồi là \[70{\rm{ }}000\] đồng.
(Giá vé tính tại thời điểm tháng 2 năm 2024)
a) Tìm các hệ số \(x\) và \(y\) trong phản ứng hóa học đã được cân bằng sau:
\(x{\rm{FeO}} + y{{\rm{O}}_2}\mathop \to \limits^{{\rm{t}}^\circ } 2{\rm{F}}{{\rm{e}}_3}{{\rm{O}}_4}.\)
Từ đó, hãy hoàn thiện phương trình phản ứng hóa học sau khi được cân bằng.
b) Giải bài toán sau bằng cách lập hệ phương trình:
Một đoàn khách du lịch gồm 40 người dự định tham quan chùa Hương (Hà Nội) bằng cáp treo khứ hồi (gồm lượt lên và lượt xuống). Nhưng khi tới nơi có 5 bạn trẻ muốn khám phá bằng đường bộ khi leo lên còn lúc xuống sẽ đi cáp treo để trải nghiệm nên 5 bạn chỉ mua vé lượt xuống, do đó đoàn đã chi ra \[8{\rm{ }}450{\rm{ }}000\] đồng để mua vé. Hỏi giá vé cáp treo khứ hồi và giá vé cáp treo 1 lượt là bao nhiêu? Biết rằng giá vé 1 lượt rẻ hơn giá vé khứ hồi là \[70{\rm{ }}000\] đồng.
(Giá vé tính tại thời điểm tháng 2 năm 2024)
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Vì số nguyên tử của \({\rm{Fe}}\) và \({\rm{O}}\) ở cả hai vế của phương trình phản ứng phải bằng nhau nên ta có hệ phương trình: \(\left\{ \begin{array}{l}x = 2 \cdot 3\\x + 2y = 2 \cdot 4\end{array} \right.\) hay \(\left\{ \begin{array}{l}x = 6\\x + 2y = 8.\end{array} \right.\)
Thay \(x = 6\) vào phương trình \(x + 2y = 8,\) ta được:
\(6 + 2y = 8,\) suy ra \(2y = 2,\) nên \(y = 1.\)
Vậy \(x = 6\) và \(y = 1.\) Khi đó ta hoàn thiện phương trình phản ứng hóa học sau cân bằng như sau:
\({\rm{6FeO}} + {{\rm{O}}_2}\mathop \to \limits^{{\rm{t}}^\circ } 2{\rm{F}}{{\rm{e}}_3}{{\rm{O}}_4}.\)
b) Gọi \(x\) (đồng) và \(y\) (đồng) lần lượt là giá vé cáp treo khứ hồi và giá vé 1 lượt \(\left( {x > 0,\,\,y > 0} \right).\)
Do giá vé 1 lượt rẻ hơn giá vé khứ hồi là \[70{\rm{ }}000\] đồng nên ta có phương trình:
\(x - y = 70\,\,000.\,\,\,\left( 1 \right)\)
Do trong đoàn \(40\) người chỉ có \(5\) người mua vé cáp treo \(1\) lượt cho lượt xuống nên đã có \(40 - 5 = 35\) người mua vé cáp treo khứ hồi.
Khi đó, số tiền cần trả để mua \(35\) vé cáp treo khứ hồi và \(5\) vé cáp treo 1 lượt là: \(35x + 5y\) (đồng).
Theo bài, cả đoàn khách du lịch này đã chi ra \[8{\rm{ }}450{\rm{ }}000\] đồng để mua vé nên ta có phương trình:
\(35x + 5y = 8{\rm{ }}450{\rm{ }}000.\,\,\,\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta có hệ phương trình: \(\left\{ \begin{array}{l}x - y = 70\,\,000\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\35x + 5y = 8{\rm{ }}450{\rm{ }}000\,\,\,\,\left( 2 \right)\end{array} \right.\)
Nhân hai vế của phương trình \(\left( 1 \right)\) với \(5,\) ta được hệ phương trình mới là: \(\left\{ \begin{array}{l}5x - 5y = 350\,\,000\\35x + 5y = 8{\rm{ }}450{\rm{ }}000.\end{array} \right.\)
Cộng từng vế hai phương trình của hệ phương trình trên, ta được:
\(40x = 8\,\,800\,\,000,\) suy ra \(x = 220\,\,000\) (thỏa mãn).
Thay \(x = 220\,\,000\) vào phương trình \(\left( 1 \right),\) ta được:
\(220\,\,000 - y = 70\,\,000,\) suy ra \(y = 150\,\,000\) (thỏa mãn).
Do đó hệ phương trình trên có nghiệm là \(\left( {x;\,\,y} \right) = \left( {220\,\,000;\,\,150\,\,000} \right).\)
Vậy giá vé cáp treo khứ hồi và giá vé cáp treo 1 lượt lần lượt là \(200\,\,000\) đồng và \(150\,\,000\) đồng.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
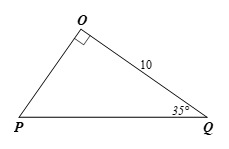
a) Xét tam giác \(OPQ\) vuông tại \(O\), ta có:
⦁ \(OQ = OQ \cdot \tan Q = 10 \cdot \tan 35^\circ \approx 7,00{\rm{\;(cm}});\)
⦁ \(OQ = PQ \cdot \cos Q\)
Suy ra \(PQ = \frac{{OQ}}{{\cos Q}} = \frac{{10}}{{\cos 35^\circ }} \approx 12,21{\rm{\;(cm)}}{\rm{.}}\)
Vậy \(OQ \approx 7,00{\rm{\;cm}},\,\,PQ \approx 12,21{\rm{\;cm}}.\)
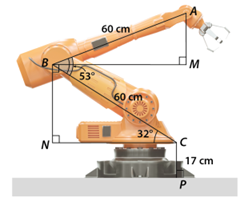
b) Xét \(\Delta BCN\) vuông tại \(N,\) ta có:
\(BN = BC \cdot \sin \widehat {BCN} = 60 \cdot \sin 32^\circ \approx 31,80{\rm{\;(cm)}}{\rm{.}}\)
Ta thấy \(NC\) và \(BM\) là các đoạn thẳng nằm trên phương ngang nên \(NC\,{\rm{//}}\,BM,\) suy ra \(\widehat {CBM} = \widehat {BCN} = 32^\circ \) (so le trong).
Khi đó, \(\widehat {ABM} = \widehat {ABC} - \widehat {CBM} = 53^\circ - 32^\circ = 21^\circ \).
Xét \(\Delta ABM\) vuông tại \(M\), ta có:
\(AM = AB \cdot \sin \widehat {ABM} = 60 \cdot \sin 21^\circ \approx 21,50\) (cm).
Vậy, độ cao của điểm \(A\) trên đầu cánh tay robot so với mặt đất là:
\(AM + BN + CP \approx 21,50 + 31,80 + 17 = 70,3\) (cm).
Lời giải
Đáp án đúng là: D
Phương trình bậc nhất hai ẩn có dạng \(ax + by = c\) với \(a \ne 0\) hoặc \(b \ne 0.\)
Phương trình \(\frac{1}{x} + 2y = - 3\) không có dạng trên, có chứa ẩn \(x\) dưới mẫu thức nên đây không phải phương trình bậc nhất hai ẩn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Chuyên đề 8: Hình học (có đáp án)
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận