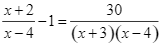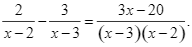Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
70 người thi tuần này 4.6 22.1 K lượt thi 17 câu hỏi 90 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
19 bài tập Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
20 bài tập Toán 9 Cánh diều Bài 2. Hình nón có đáp án
Danh sách câu hỏi:
Lời giải
Đáp án đúng là: D
Phương trình bậc nhất hai ẩn có dạng ![]() với
với ![]() hoặc
hoặc ![]() .
.
Do đó, ![]() không là phương trình bậc nhất hai ẩn.
không là phương trình bậc nhất hai ẩn.
Lời giải
Đáp án đúng là: A
Vì ![]() khi
khi ![]() và
và ![]() khi
khi ![]() nên điều kiện xác định của phương trình đã cho là
nên điều kiện xác định của phương trình đã cho là ![]() và
và ![]() .
.
Lời giải
Đáp án đúng là: B
Bất đẳng thức diễn tả khẳng định “![]() nhỏ hơn
nhỏ hơn ![]() ” là
” là ![]()
Lời giải
Đáp án đúng là: A
Điều kiện xác định của biểu thức ![]() là
là ![]() hay
hay ![]()
Lời giải
Đáp án đúng là: A
Ta có ![]() . Mà
. Mà ![]() , do đó
, do đó ![]()
Vậy ![]() .
.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
|
(1,0 điểm) Một người có tầm mắt cao \[1,65{\rm{ m}}\] đứng trên tầng thượng của tòa Lotte Center thì nhìn thấy một chiếc xe thu gom phế thải đang dừng ở \[B\] với góc nghiêng \[80^\circ \] (như hình vẽ). Biết xe đó cách tòa nhà \(48{\rm{ m}}\). a) Tính chiều cao của tòa nhà Lotte Center. b) Một người ở độ cao \[200{\rm{ m}}\] của tòa nhà cũng nhìn thấy xe thu gom phế thải khác đang dừng ở \[E\] với góc nghiêng \(65^\circ \). Hỏi hai xe thu gom phế thải cách nhau bao nhiêu mét? (tất cả các kết quả làm tròn đến hàng phần trăm) |
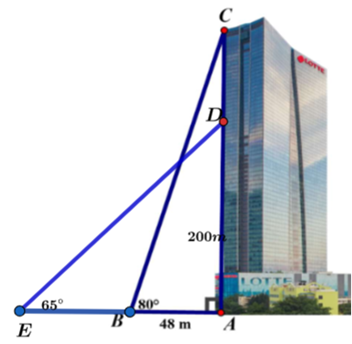 |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.