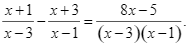Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 09
51 người thi tuần này 4.6 22.1 K lượt thi 9 câu hỏi 90 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
19 bài tập Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
20 bài tập Toán 9 Cánh diều Bài 2. Hình nón có đáp án
Danh sách câu hỏi:
Lời giải
⦁ Ta có căn bậc hai của ![]() là
là ![]() .
.
Vậy căn bậc hai của ![]() là
là ![]() .
.
⦁ Vì ![]() có căn bậc hai là
có căn bậc hai là ![]() , nên ta có:
, nên ta có:
![]() suy ra
suy ra ![]() hay
hay ![]() .
.
Vậy ![]() là số cần tìm.
là số cần tìm.
Lời giải
Hướng dẫn giải
a) Với mọi \(x \ge 0,\) ta có:
⦁ \[\sqrt x - 3 \ne 0\] khi \(\sqrt x \ne 3\) hay \(x \ne 9.\)
⦁ \(x - 1 = \left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)\) và \(1 - \sqrt x = - \left( {\sqrt x - 1} \right)\)
Với mọi \(x \ge 0,\) ta có \(\sqrt x \ge 0\) nên \(\sqrt x + 1 \ge 1 > 0.\)
Do đó \(x - 1 \ne 0\) khi \(\sqrt x - 1 \ne 0,\) hay \(\sqrt x \ne 1,\) tức là \(x \ne 1.\)
Như vậy, điều kiện xác định của biểu thức \[A = \frac{{\sqrt x - 1}}{{\sqrt x - 3}}\] là \[x \ge 0,\,\,x \ne 9\] và điều kiện xác định của biểu thức \[B = \frac{{\sqrt x + 3}}{{\sqrt x + 1}} - \frac{5}{{1 - \sqrt x }} + \frac{4}{{x - 1}}\] là \[x \ge 0,\,\,x \ne 1.\]
b) Thay \[x = \frac{1}{9}\] (thỏa mãn điều kiện) vào biểu thức \[A\], ta được:
\[A = \frac{{\sqrt {\frac{1}{9}} - 1}}{{\sqrt {\frac{1}{9}} - 3}} = \frac{{\frac{1}{3} - 1}}{{\frac{1}{3} - 3}} = \frac{{ - \frac{2}{3}}}{{ - \frac{8}{3}}} = \frac{1}{4}.\]
Vậy \(A = \frac{1}{4}\) khi \(x = \frac{1}{9}.\)
c) Với \[x \ge 0;x \ne 1\], ta có:
\[B = \frac{{\sqrt x + 3}}{{\sqrt x + 1}} - \frac{5}{{1 - \sqrt x }} + \frac{4}{{x - 1}}\]
\[ = \frac{{\sqrt x + 3}}{{\sqrt x + 1}} + \frac{5}{{\sqrt x - 1}} + \frac{4}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\]
\[ = \frac{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} + \frac{{5\left( {\sqrt x + 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} + \frac{4}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\]
\[ = \frac{{x + 2\sqrt x - 3 + 5\sqrt x + 5 + 4}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\]
\[ = \frac{{x + 7\sqrt x + 6}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\]\[ = \frac{{x + \sqrt x + 6\sqrt x + 6}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\]
\[ = \frac{{\left( {\sqrt x + 1} \right)\left( {\sqrt x + 6} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} = \frac{{\sqrt x + 6}}{{\sqrt x - 1}}\].
Vậy với \[x \ge 0;x \ne 1\] thì \[B = \frac{{\sqrt x + 6}}{{\sqrt x - 1}}\].
d) Với \[x \ge 0,\,\,x \ne 1,x \ne 9,\] ta có:
\[P = A \cdot B = \frac{{\sqrt x - 1}}{{\sqrt x - 3}} \cdot \frac{{\sqrt x + 6}}{{\sqrt x - 1}} = \frac{{\sqrt x + 6}}{{\sqrt x - 3}} = \frac{{\sqrt x - 3 + 9}}{{\sqrt x - 3}} = 1 + \frac{9}{{\sqrt x - 3}}.\]
⦁ Với \[0 \le x < 9,x \ne 1\] thì \[\sqrt x - 3 < 0\], suy ra \[1 + \frac{9}{{\sqrt x - 3}} < 1\] hay \[P < 1.\]
⦁ Với \[x > 9\] và \[x \in \mathbb{N}\] suy ra \[x \ge 10\]. Do đó, \[\sqrt x - 3 \ge \sqrt {10} - 3 > 0\].
Suy ra \[\frac{9}{{\sqrt x - 3}} \le \frac{9}{{\sqrt {10} - 3}}\] nên \[1 + \frac{9}{{\sqrt x - 3}} \le 1 + \frac{9}{{\sqrt {10} - 3}}\] hay \[P \le 1 + \frac{9}{{\sqrt {10} - 3}}\].
Dấu “=” xảy ra khi \[x = 10\].
Vậy với \[x = 10\] thì biểu thức \[P\] đạt giá trị lớn nhất.
Lời giải
Điều kiện xác định: \[x \ne 1;x \ne 3\].
Ta có: \[\frac{{x + 1}}{{x - 3}} - \frac{{x + 3}}{{x - 1}} = \frac{{8x - 5}}{{\left( {x - 3} \right)\left( {x - 1} \right)}}\]
\[\frac{{\left( {x + 1} \right)\left( {x - 1} \right) - \left( {x + 3} \right)\left( {x - 3} \right)}}{{\left( {x - 3} \right)\left( {x - 1} \right)}} = \frac{{8x - 5}}{{\left( {x - 3} \right)\left( {x - 1} \right)}}\]
\[\frac{{{x^2} - 1 - \left( {{x^2} - 9} \right)}}{{\left( {x - 3} \right)\left( {x - 1} \right)}} = \frac{{8x - 5}}{{\left( {x - 3} \right)\left( {x - 1} \right)}}\]
\[{x^2} - 1 - {x^2} + 9 = 8x - 5\]
\[8 = 8x - 5\]
\[8x = 13\]
\[x = \frac{{13}}{8}\] (thỏa mãn).
Vậy phương trình có nghiệm là \[x = \frac{{13}}{8}\].Lời giải
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Vậy bất phương trình có nghiệm là ![]()
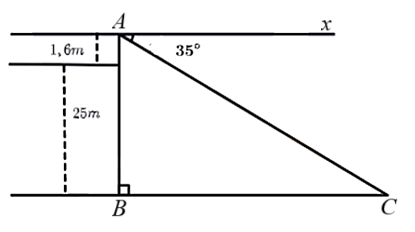
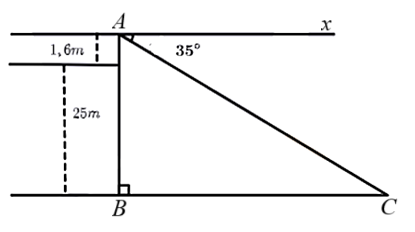
Câu 5
Giải bài toán sau bằng cách lập hệ phương trình:
Giá niêm yết của một chiếc bếp từ đôi và một chiếc nồi chiên không dầu tổng cộng là 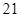 triệu đồng. Nhân dịp khuyến mãi cuối năm, cửa hàng giảm giá bếp từ đôi
triệu đồng. Nhân dịp khuyến mãi cuối năm, cửa hàng giảm giá bếp từ đôi 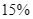 và nồi chiên không dầu giảm giá
và nồi chiên không dầu giảm giá 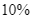 so với giá niêm yết nên bác Lan đi mua hai sản phẩm này chỉ hết
so với giá niêm yết nên bác Lan đi mua hai sản phẩm này chỉ hết 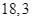 triệu. Tính giá niêm yết của mỗi sản phẩm.
triệu. Tính giá niêm yết của mỗi sản phẩm.
Giải bài toán sau bằng cách lập hệ phương trình:
Giá niêm yết của một chiếc bếp từ đôi và một chiếc nồi chiên không dầu tổng cộng là ![]() triệu đồng. Nhân dịp khuyến mãi cuối năm, cửa hàng giảm giá bếp từ đôi
triệu đồng. Nhân dịp khuyến mãi cuối năm, cửa hàng giảm giá bếp từ đôi ![]() và nồi chiên không dầu giảm giá
và nồi chiên không dầu giảm giá ![]() so với giá niêm yết nên bác Lan đi mua hai sản phẩm này chỉ hết
so với giá niêm yết nên bác Lan đi mua hai sản phẩm này chỉ hết ![]() triệu. Tính giá niêm yết của mỗi sản phẩm.
triệu. Tính giá niêm yết của mỗi sản phẩm.
Lời giải
Gọi \[x,\,\,y\] (triệu đồng) lần lượt là giá niêm yết của một chiếc bếp từ đôi và một chiếc nồi chiên không dầu \[\left( {0 < x < 21,\,\,0 < y < 21} \right).\]
Theo đề, giá niêm yết của một chiếc bếp từ đôi và một chiếc nồi chiên không dầu tổng cộng là ![]() triệu đồng nên ta có phương trình:
triệu đồng nên ta có phương trình: ![]() . (1)
. (1)
Bếp từ đôi giảm giá ![]() , tức là có giá bằng
, tức là có giá bằng ![]() giá niêm yết , nghĩa là giá của một bếp từ đôi sau khi giảm là
giá niêm yết , nghĩa là giá của một bếp từ đôi sau khi giảm là ![]() .
.
Nồi chiên không dầu giảm giá ![]() , tức là có giá bằng
, tức là có giá bằng ![]() giá niêm yết, nghĩa là giá của một nồi chiên không dầu sau khi giảm là
giá niêm yết, nghĩa là giá của một nồi chiên không dầu sau khi giảm là ![]() .
.
Bác Lan mua hai sản phẩm sau khi giảm giá với số tiền ![]() triệu đồng nên ta có phương trình:
triệu đồng nên ta có phương trình:
![]() . (2)
. (2)
Từ (1) và (2) ta có hệ phương trình: 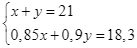 .
.
Từ phương trình thứ nhất, ta có: ![]() , thế vào phương trình thứ hai, ta được:
, thế vào phương trình thứ hai, ta được:
![]()
![]()
![]()
![]() (thỏa mãn).
(thỏa mãn).
Thay ![]() vào phương trình (*), ta được
vào phương trình (*), ta được ![]() (thỏa mãn).
(thỏa mãn).
Vậy giá niêm yết của bếp từ đôi và nồi chiên không dầu lần lượt là ![]() triệu đồng và
triệu đồng và ![]() triệu đồng.
triệu đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.