10 bài tập Chứng minh tứ giác nội tiếp một đường tròn có lời giải
69 người thi tuần này 4.6 376 lượt thi 10 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
19 bài tập Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
20 bài tập Toán 9 Cánh diều Bài 2. Hình nón có đáp án
Danh sách câu hỏi:
Câu 1
A. Hình thoi.
B. Hình bình hành.
C. Hình thang.
D. Hình chữ nhật.
Lời giải
Đáp án đúng là: D
Hình chữ nhật là một tứ giác nội tiếp đường tròn, có tâm là giao điểm của hai đường chéo và bán kính bằng một nửa độ dài đường chéo.
Câu 2
A. Tứ giác ADHE là tứ giác nội tiếp.
B. Tứ giác BCDE là tứ giác nội tiếp.
C. Cả A và B đều đúng.
D. Cả A và B đều sai.
Lời giải
Đáp án đúng là: C
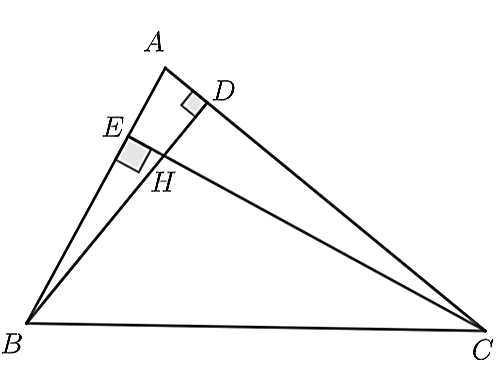
Vì BD, CE là các đường cao của ∆ABC nên BD
⊥ AC và CE ⊥ AB.Suy ra \[\widehat {AEH} = \widehat {ADH} = 90^\circ \].
Xét ∆AEH vuông tại E nên H, E, A thuộc đường tròn đường kính AH (1)
Xét ∆ADH vuông tại D nên D, A, H thuộc đường tròn đường kính AH (2).
Từ (1) và (2) suy ra A, E, D, H cùng thuộc một đường tròn.
Suy ra ADHE là tứ giác nội tiếp.
Xét tứ giác BCDE. Gọi O là trung điểm của BC.
Vì BD, CE là các đường cao của ∆ABC nên DB ⊥ AC và CE ⊥ AB.
Suy ra \[\widehat {BDC} = \widehat {BEC} = 90^\circ \].
Xét tam giác BDC, có \[\widehat {BDC} = 90^\circ \] và DO là trung tuyến nên OD = OC = OB = \[\frac{1}{2}BC\].
Xét tam giác BEC có \[\widehat {BEC} = 90^\circ \] và EO là trung tuyến nên OE = OC = OB = \[\frac{1}{2}BC\].
Từ đấy suy ra OE = OC = OB = OD.
Vậy tứ giác BCDE nội tiếp đường tròn tâm O là trung điểm BC.
Lời giải
Đáp án đúng là: C
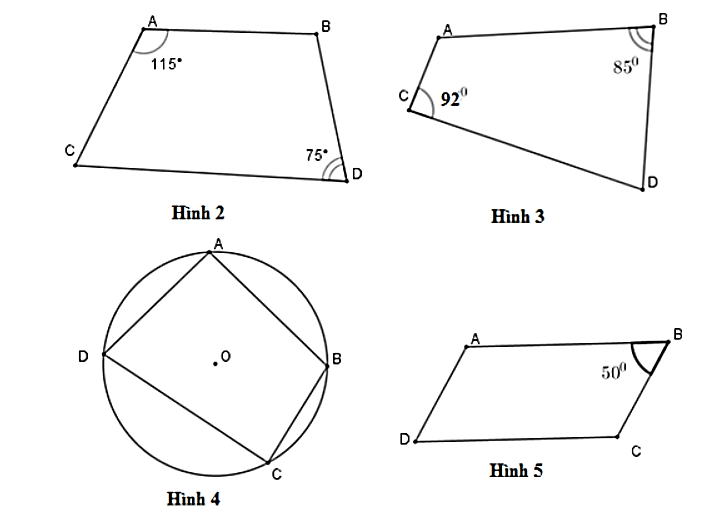
Trong các hình trên, nhận thấy Hình 4 là tứ giác nội tiếp.
Câu 4
A. AHCK là tứ giác nội tiếp.
B. AHCK không nội tiếp đường tròn.
C. \[\widehat {EAO} = \widehat {HCK}\].
D. AH.AB = AD.BD.
Lời giải
Đáp án đúng là: A
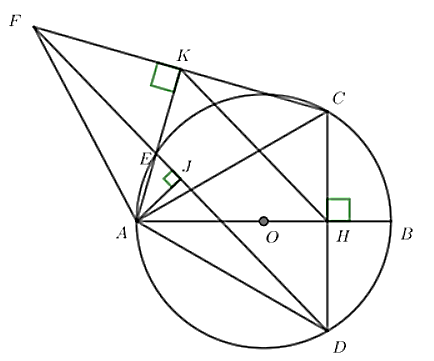
Xét (O) có CH
⊥ AB (gt) nên \[\widehat {CHA} = 90^\circ \]; CK ⊥ AK (gt) nên \[\widehat {CKA} = 90^\circ \].Có ∆CAH vuông tại H nên H, A, C cùng thuộc đường tròn đường kính AC.
Có ∆CKA vuông tại K nên K, A, C cùng thuộc đường tròn đường kính AC.
Do đó, K, H, A, C cùng thuộc đường tròn đường kính AC.
Suy ra AHCK là tứ giác nội tiếp.
Chứng minh được ∆HAD ᔕ ∆DAB (g.g) nên \[\frac{{AH}}{{AD}} = \frac{{AD}}{{AB}}\] hay AH.AB = AD2.
Câu 5
A. Hình thang.
B. Hình thang cân.
C. Tứ giác nội tiếp.
D. Hình bình hành.
Lời giải
Đáp án đúng là: C
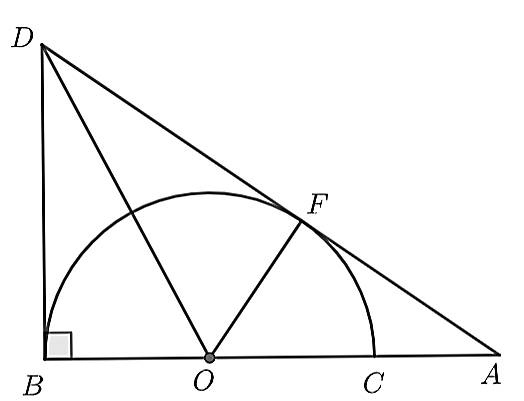
Xét tứ giác BDFO, có:
\[\widehat {DBO} = \widehat {OFD} = 90^\circ \] nênbốn điểm B, O, D, F cùng thuộc đường tròn đường kính DO.
Hay BOFD là tứ giác nội tiếp.
Câu 6
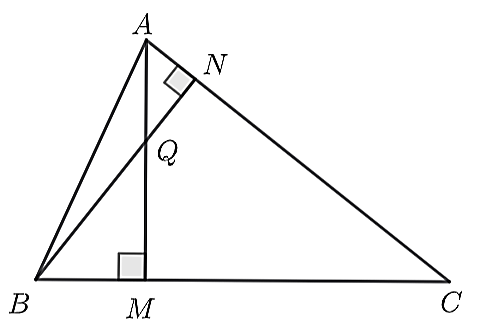
A. Bốn điểm M, Q, N, C nằm trên một đường tròn.
B. Bốn điểm A, N, M, B nằm trên một đường tròn.
C. Đường tròn qua ANB có tâm là trung điểm của đoạn AB.
D. Bốn điểm A, B, M, C nằm trên một đường tròn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. MICH là hình chữ nhật.
B. MICH là hình vuông.
C. MICH không là tứ giác nội tiếp.
D. MICH là tứ giác nội tiếp.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
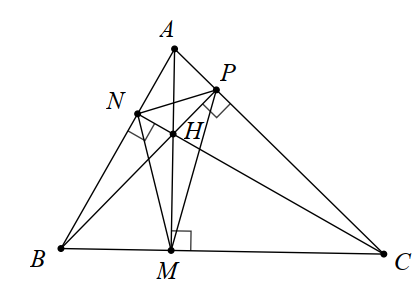
A. Có 3 tứ giác nội tiếp.
B. Có 4 tứ giác nội tiếp.
C. Có 5 tứ giác nội tiếp.
D. Có 6 tứ giác nội tiếp.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
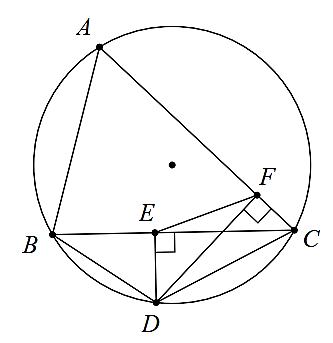
A. Tứ giác ABDC nội tiếp đường tròn.
B. Tứ giác DEFC nội tiếp đường tròn.
C. \[\widehat {DEF} + \widehat {FCD} = 180^\circ \].
D. Tứ giác DEFC không nội tiếp đường tròn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. Chỉ (I) đúng.
B. Chỉ (II) đúng.
C. Cả (I), (II) đều đúng.
D. Cả (I), (II) đều sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.