4 bài tập Tính góc của tứ giác nội tiếp đường tròn (có lời giải)

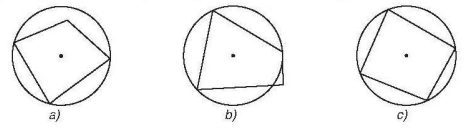
Ở hình a) và hình b), tứ giác không nội tiếp đường tròn vì có một đỉnh tứ giác không nằm trên đường tròn

Ở hình c), tứ giác nội tiếp đường tròn vì 4 đỉnh tứ giác nằm trên đường tròn

a) Ta có: \[\widehat {ABC} = \frac{1}{2}\alpha  = \frac{1}{2}{.140^0} = {70^0}\] (góc nội tiếp và góc ở tâm cùng chắn cung\[AC\])

\[\widehat {ABC} + \widehat {ADC} = {180^0}\](tứ giác\[ABCD\] nội tiếp đường tròn )

\[\begin{array}{l}{70^0} + \widehat {ADC} = {180^0}\\\widehat {ADC} = {180^0} - {70^0}\\\widehat {ADC} = {110^0}\end{array}\]

b) tứ giác\[ABCD\] nội tiếp đường tròn nên \[\widehat {BAD} + \widehat {BCD} = {180^0}\].

a) Ta có:

\[\widehat {ABC} + \widehat {ADC} = {180^0}\](tứ giác\[ABCD\] nội tiếp đường tròn )

\[\begin{array}{l}\widehat {ABC} + {40^0} = {180^0}\\\widehat {ABC} = {180^0} - {40^0}\\\widehat {ABC} = {140^0}\end{array}\]

\[\widehat {BAD} + \widehat {BCD} = {180^0}\](tứ giác\[ABCD\] nội tiếp đường tròn )

\[\begin{array}{l}\widehat {BAD} + {100^0} = {180^0}\\\widehat {BAD} = {180^0} - {100^0}\\\widehat {BAD} = {80^0}\end{array}\]

b) Ta có:

\[\widehat {AXD} + \widehat {XAD} + \widehat {XDA} = {180^0}\](tổng ba góc của tam giác\[ADX\])

\[\begin{array}{l}\widehat {AXD} + {80^0} + {40^0} = {180^0}\\\widehat {AXD} = {180^0} - \left( {{{80}^0} + {{40}^0}} \right)\\\widehat {AXD} = {60^0}\end{array}\]

a)

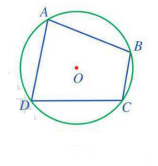
- Ta có: \[\widehat A + \widehat C = {180^0}\](tứ giác\[ABCD\] nội tiếp đường tròn )

\[\begin{array}{l}{45^0} + \widehat C = {180^0}\\\widehat C = {180^0} - {45^0}\\\widehat C = {135^0}\end{array}\]

- Ta có: \[\widehat B + \widehat D = {180^0}\](tứ giác\[ABCD\] nội tiếp đường tròn )

\[\begin{array}{l}{155^0} + \widehat D = {180^0}\\\widehat D = {180^0} - {155^0}\\\widehat D = {25^0}\end{array}\]

b) \(\widehat B = {60^0}\) và \(\widehat C = {85^0}\).

- Ta có: \[\widehat B + \widehat D = {180^0}\](tứ giác\[ABCD\] nội tiếp đường tròn )

\[\begin{array}{l}{60^0} + \widehat D = {180^0}\\\widehat D = {180^0} - {60^0}\\\widehat D = {120^0}\end{array}\]

- Ta có: \[\widehat A + \widehat C = {180^0}\](tứ giác\[ABCD\] nội tiếp đường tròn )

\[\begin{array}{l}\widehat A + {85^0} = {180^0}\\\widehat A = {180^0} - {85^0}\\\widehat A = {95^0}\end{array}\]