21 bài tập Toán 9 Kết nối tri thức Bài 29. Tứ giác nội tiếp có đáp án

99 người thi tuần này 4.6 225 lượt thi 21 câu hỏi 45 phút

Câu 1/21

Trong các tứ giác sau, tứ giác nào nội tiếp được đường tròn? Giải thích.

Xem đáp án

Lời giải

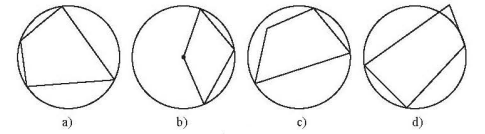
Ở hình a) và hình b), tứ giác nội tiếp đường tròn vì 4 đỉnh tứ giác nằm trên đường tròn

Ở hình c) và hình d), tứ giác không nội tiếp đường tròn vì có một đỉnh tứ giác không nằm trên đường tròn

Câu 2/21

Trong các đường tròn \[\left( O \right)\] sau, đường tròn nào ngoại tiếp tứ giác \[ABCD\] ? Giải thích.

$Trong các đường tròn \[\left( O \right)\] sau, đường tròn nào ngoại tiếp tứ giác \[ABCD\] ? Giải thích. (ảnh 1)$

Xem đáp án

Lời giải

Lời giải

Ở hình 1) và hình 3), đường tròn \[\left( O \right)\] là đường tròn ngoại tiếp tứ giác \[ABCD\] vì nó đi qua cả bốn đỉnh của tứ giác \[ABCD\].

Ở hình 2), đường tròn \[\left( O \right)\] là đường tròn không ngoại tiếp tứ giác \[ABCD\] vì nó không đi qua đỉnh \[D\] của tứ giác.

Câu 3/21

Cho tam giác $ABC$ có 3 góc nhọn nội tiếp đường tròn $(O)$ có trực tâm là điểm $H$. Gọi $M$ là điểm trên dây cung $BC$ không chứa điểm $A$( $M$ khác $B,C$). Gọi $N,P$ theo thứ tự là các điểm đối xứng của $M$ qua các đường thẳng $AB,AC$

a) Chứng minh \[AHCP\] là tứ giác nội tiếp

b) Chứng minh $N,H,P$ thẳng hàng.

Xem đáp án

Lời giải

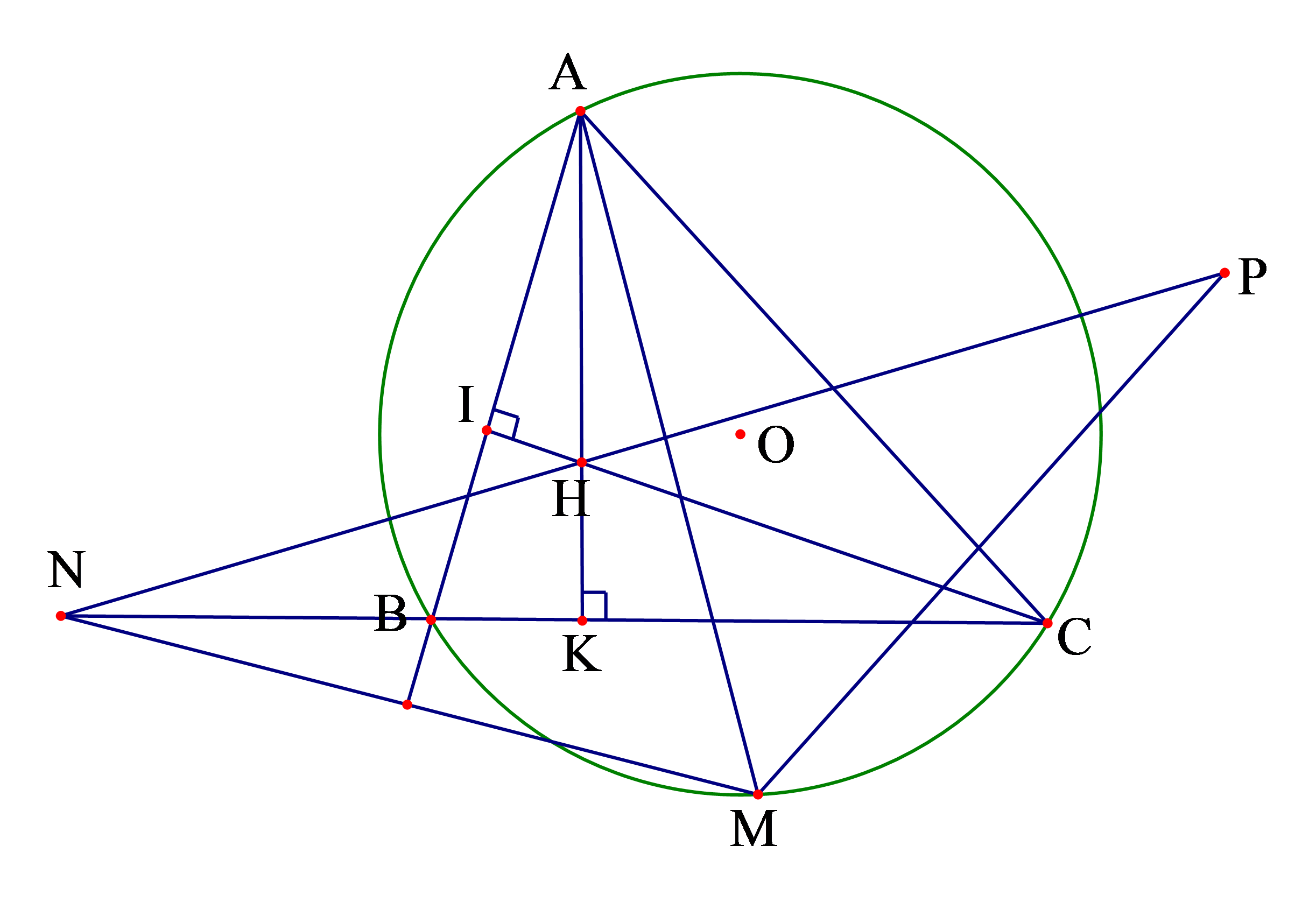
$Cho tam giác $ABC$ có 3 góc nhọ (ảnh 1)$

a). Giả sử các đường cao của tam giác là $AK,CI$ . Để chứng minh $AHCP$ là tứ giác nội tiếp ta sẽ chứng minh $\widehat {AHC} + \widehat {APC} = {180^0}$.

Ta có:

$\widehat {AHC} = \widehat {IHK}$ ( đối đỉnh)

$\widehat {APC} = \widehat {AMC} = \widehat {ABC}$ ( do tính đối xứng và góc nội tiếp cùng chắn một cung).

Như vậy ta chỉ cần chứng minh $\widehat {ABC} + \widehat {IHK} = {180^0}$ nhưng điều này là hiển nhiên do tứ giác $BIHK$là tứ giác nội tiếp.

b). Để chứng minh $N,H,P$ thẳng hàng ta sẽ chứng minh $\widehat {NHA} + \widehat {AHP} = {180^0}$ do đó ta sẽ tìm cách quy hai góc này về 2 góc đối nhau trong một tứ giác nội tiếp.

Thật vậy ta có: $\widehat {AHP} = \widehat {ACP}$ (tính chất góc nội tiếp), $\widehat {ACP} = \widehat {ACM}$ (1) (Tính chất đối xứng) .

Ta thấy vai trò tứ giác $AHCP$ giống với $AHBN$ nên ta cũng dễ chứng minh được $AHBN$ là tứ giác nội tiếp từ đó suy ra $\widehat {AHN} = \widehat {ABN}$ , mặt khác $\widehat {ABN} = \widehat {ABM}$ (2) (Tính chất đối xứng) .

Từ (1), (2) ta suy ra chỉ cần chứng minh $\widehat {ABM} + \widehat {ACM} = {180^0}$ nhưng điều này là hiển nhiên do tứ giác $ABMC$ nội tiếp.

Vậy $\widehat {NHA} + \widehat {AHP} = {180^0}$ hay $N,H,P$ thẳng hàng.

Câu 4/21

Cho đường tròn $\left( {O;R} \right)$ và điểm $A$ ở bên ngoài đường tròn. Vẽ hai tiếp tuyến \[AB,AC\] với đường tròn $\left( O \right)$ ($B,C$ là các tiếp điểm). Gọi $M$ là trung điểm $AB$.

     a) Chứng minh tứ giác $ABOC$ nội tiếp và xác định tâm $I$ của đường tròn này.

     b) Chứng minh rằng $AM.AO = AB.AI$.

     c) Gọi $G$ là trọng tâm tam giác $ACM$. Chứng minh $MG//BC$.

     d) Chứng minh $IG$ vuông góc với $CM$.

Xem đáp án

Lời giải

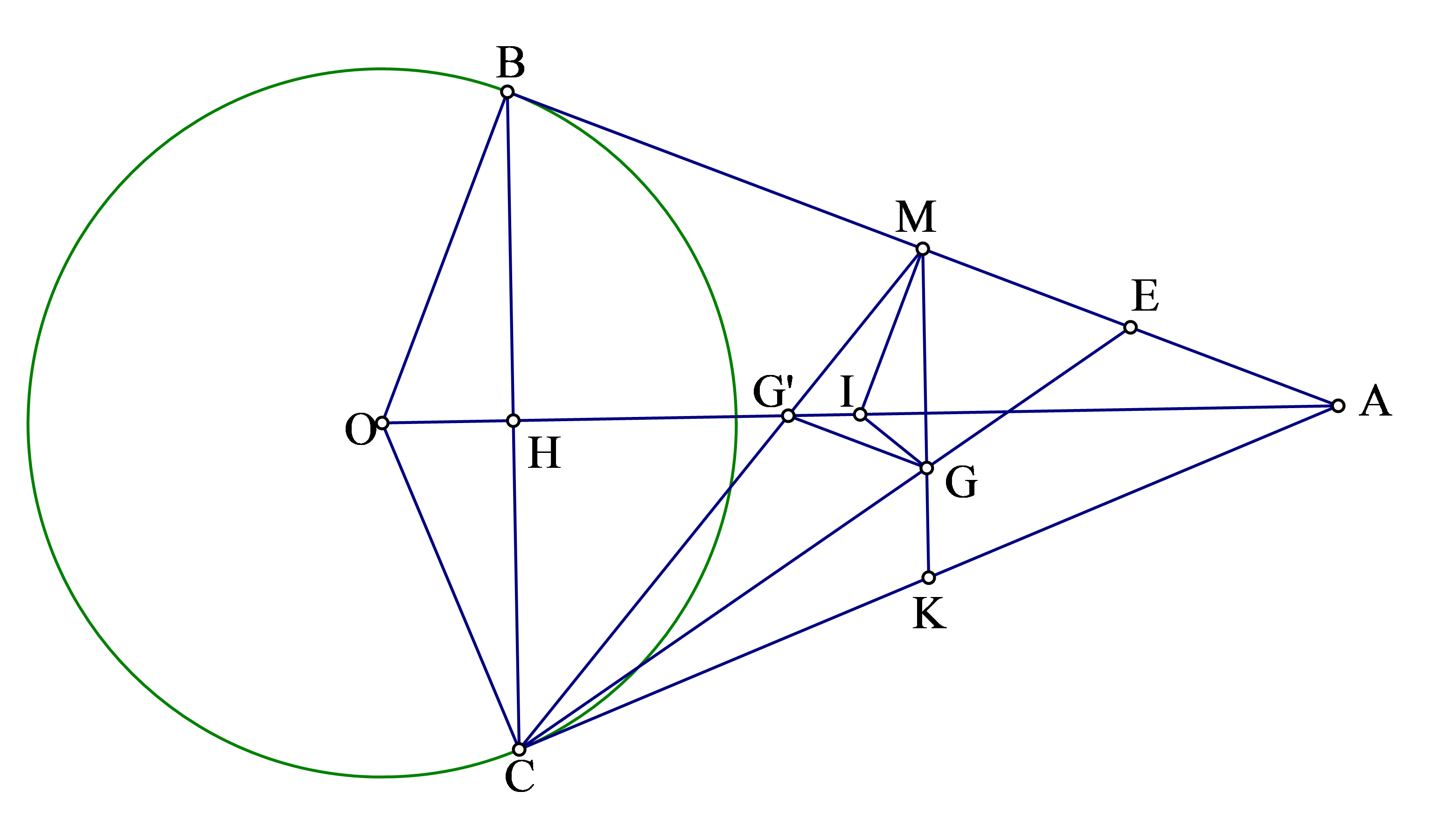
$Cho đường tròn $\left( {O;R} \right)$ và điểm \(A\ (ảnh 1)$

a) Do $AB,AC$ là hai tiếp tuyến cắt nhau của đường tròn $\left( O \right)$ nên $\widehat {ABO} = \widehat {ACO} = {90^0} \Rightarrow B,C$ thuộc đường tròn đường kính $OA$ có tâm $I$ là trung điểm $OA$.

b) Ta có $AM.AO = \frac{{AB}}{2}.2AI = AB.AI$.

c) Gọi $E$ là trung điểm $MA$, do $G$ là trọng tâm $\Delta CMA$ nên $G \in CE$ và $\frac{{GE}}{{CE}} = \frac{1}{3}$.

Mặt khác $\frac{{ME}}{{BE}} = \frac{1}{3}$ (vì $ME = \frac{{MA}}{2} = \frac{{MB}}{2}$ nên $ME = \frac{{BE}}{3}$) $ \Rightarrow \frac{{GE}}{{CE}} = \frac{{ME}}{{BE}}$, theo định lý Ta-lét đảo $ \Rightarrow MG//BC$.

d) Gọi $G'$ là giao điểm của $OA$ và $CM \Rightarrow G'$ là trọng tâm $\Delta ABC$. Nên $\frac{{G'M}}{{CM}} = \frac{1}{3} = \frac{{GE}}{{CE'}}$, theo định lý Ta-lét đảo $GG'//ME$ (1)

$MI$ là đường trung bình trong $\Delta OAB \Rightarrow MI//OB$, mà $AB \bot OB$ (cmt) $ \Rightarrow MI \bot AB$, nghĩa là $MI \bot ME$ (2).

Từ (1) và (2) cho $MI \bot GG'$, ta lại có $GI' \bot MK$ (vì $OA \bot MK$) nên $I$ là trực tâm $\Delta MGG'$$ \Rightarrow GI \bot G'M$ tức $GI \bot CM$.

Câu 5/21

Cho tam giác $ABC$ và đường cao $AH$ gọi $M,N$ lần lượt là trung điểm của $AB,AC$. Đường tròn ngoại tiếp tam giác $BHM$ cắt đường tròn ngoại tiếp tam giác $CNH$ tại $E$. Chứng minh $AMEN$ là tứ giác nội tiếp và $HE$ đi qua trung điểm của $MN$.

Xem đáp án

Lời giải

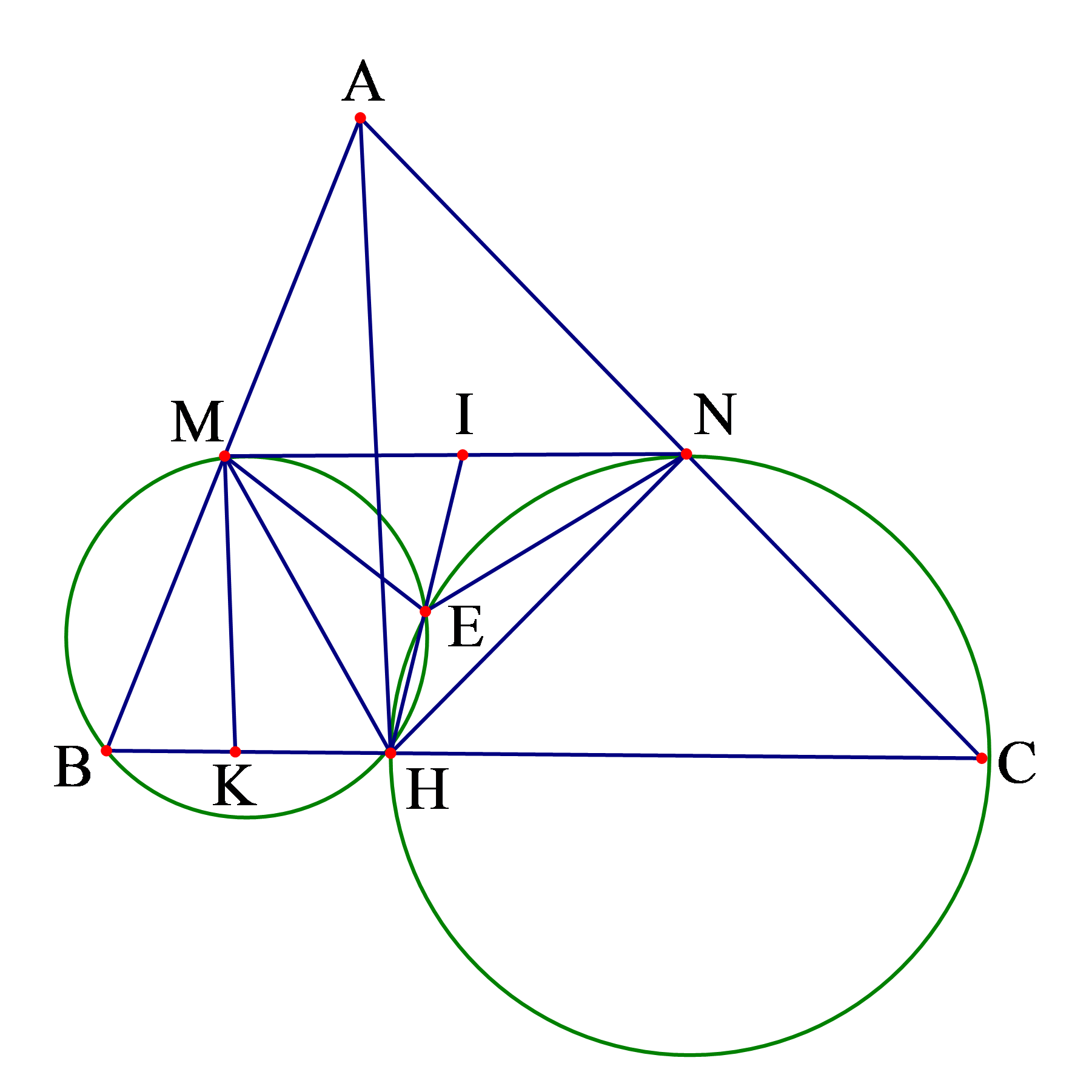
$Cho tam giác $ABC$ và đường cao $AH$ gọi \( (ảnh 1)$

Để chứng minh $AMEN$ là tứ giác nội tiếp ta sẽ

chứng minh: $\widehat {MAN} + \widehat {MEN} = {180^0}$.

Ta cần tìm sự liên hệ của các góc $\widehat {MAN};\widehat {MEN}$ với các góc có sẵn của những tứ giác nội tiếp khác.

Ta có $\widehat {MEN} = {360^0} - \left( {\widehat {MEH} + \widehat {NEH}} \right) = {360^0} - \left( {{{180}^0} - \widehat {ABC} + {{180}^0} - \widehat {ACB}} \right) = \widehat {ABC} + \widehat {ACB}$ $ = {180^0} - \widehat {BAC}$ suy ra $\widehat {MEN} + \widehat {MAN} = {180^0}$. Hay tứ giác $AMEN$ là tứ giác nội tiếp.

Kẻ $MK \bot BC$, giả sử $HE$ cắt $MN$ tại $I$ thì $IH$ là cát tuyến của hai đường tròn $(BMH)$, $(CNH)$.

Lại có $MB = MH = MA$ (Tính chất trung tuyến tam giác vuông).

Suy ra tam giác $MBH$ cân tại $M \Rightarrow KB = KH \Rightarrow MK$ luôn đi qua tâm đường tròn ngoại tiếp tam giác $MBH$. Hay $MN$ là tiếp tuyến của $(MBH)$ suy ra $I{M^2} = IE.IH$, tương tự ta cũng có $MN$ là tiếp tuyến của $\left( {HNC} \right)$ suy ra $I{N^2} = IE.IH$ do đó $IM = IN$.

Câu 6/21

Trên các cạnh $BC,CD$ của hình vuông $ABCD$ ta lấy lần lượt các điểm $M,N$ sao cho $\widehat {MAN} = {45^0}$. Đường thẳng $BD$ cắt các đường thẳng $AM,AN$ tương ứng tại các điểm $P,Q$.

a) Chứng minh rằng các tứ giác $ABMQ$ và $ADNP$ nội tiếp.

b) Chứng minh rằng các điểm $M,N,Q,P,C$ nằm trên cùng một đường tròn.

Xem đáp án

Lời giải

$Trên các cạnh $BC,CD$ của hìn (ảnh 1)$

a). Gọi $E$ là giao điểm của $AN$ và $BC$.

Các điểm $M$ và $Q$ nằm trên hai cạnh$EB$ và $EA$ của tam giác $EBA$, nên tứ giác$ABMQ$ là lồi. Các đỉnh $A$ và $B$ cùng nhìn đoạn thẳng $MQ$ dưới một góc ${45^0}$ không đổi. Vì vậy tứ giác $ABMQ$ nội tiếp.

Lập luận tương tự ta suy ra tứ giác $ADNP$ nội tiếp.

b) Từ kết quả câu a, suy ra $\widehat {ADP} = \widehat {ANP} = {45^0},\widehat {QAM} = \widehat {QBM} = {45^0}$$ \Rightarrow NP \bot AM,MQ \bot AN$. Tập hợp các điểm $P,Q,C$ nhìn đoạn $MN$ dưới một góc vuông, nên các điểm này nằm trên đường tròn đường kính $MN$.

Câu 7/21

Cho điểm $M$ thuộc cung nhỏ $BC$ của đường tròn $\left( O \right)$. Một đường thẳng $d$ở ngoài $\left( O \right)$ và vuông góc với $OM$; $CM,BM$ cắt $d$ lần lượt tại \[D,E\]. Chứng minh rằng $B,C,D,E$ cùng thuộc một đường tròn.

Xem đáp án

Lời giải

$Cho điểm $M$ thuộc cung nhỏ $BC$ của (ảnh 1)$

Kẻ đường kính $AM$ cắt $d$ tại $N$.

Ta có $\widehat {ANE} = \widehat {ABE} = {90^0}$ nên tứ giác $ABNE$ nội tiếp, suy ra $\widehat {BEN} = \widehat {BAN}$.

Mặt khác $\widehat {BAN} = \widehat {BCM}$, do đó $\widehat {BCM} = \widehat {BEN}$ hay $\widehat {BCD} = \widehat {BED}$.

Tứ giác $BCDE$ có các đỉnh $C$ và $E$ cùng nhìn đoạn thẳng $BD$ dưới một góc không đổi. Vì vậy tứ giác $BCDE$ nội tiếp.

Vậy $B,C,D,E$ cùng thuộc một đường tròn.

Câu 8/21

Cho đường tròn $\left( {O;R} \right)$ nội tiếp $\Delta ABC$, tiếp xúc với cạnh $AB,AC$ lần lượt ở $D$ và$E$

a) Gọi $O'$ là tâm đường tròn nội tiếp $\Delta ADE$, tính $OO'$ theo $R$.

b) Các đường phân giác trong của $\widehat B$ và $\widehat C$ cắt đường thẳng $DE$ lần lượt tại $M$ và $N$. Chứng minh tứ giác $BCMN$ nội tiếp được đường tròn.

c) Chứng minh $\frac{{MN}}{{BC}} = \frac{{DM}}{{AC}} = \frac{{EN}}{{AB}}$.

Xem đáp án

Lời giải

$Cho đường tròn \(\left( {O;R} (ảnh 1)$

a). Gọi $O'$ là giao điểm của $AO$ với cung nhỏ $DE$ của đường tròn $\left( O \right) \Rightarrow O'$ thuộc đường phân giác

của $\widehat A$ trong $\Delta ADE$.

Ta có $\widehat {DOA} = \widehat {EOA}$ (tính chất hai tiếp tuyến cắt nhau) $ \Rightarrow \widehat {DO'} = \widehat {O'E}$.

Mà $ \Rightarrow \widehat {ADO'} = \widehat {EDO'}$$ \Rightarrow DO'$ là phân giác $\widehat D$$ \Rightarrow O'$ là tâm đường tròn nội tiếp $\Delta ADE$. Do đó $OO' = R$.

b) Do $AB = AC$ (tính chất hai tiếp tuyến cắt nhau) $ \Rightarrow \Delta ADE$ cân tại $A$ nên $\widehat {ADE} = \frac{{{{180}^0} - \widehat {BAC}}}{2} = {90^0} - \frac{{\widehat {BAC}}}{2}$.

Mà $\widehat {ADE} = \widehat {ABM} + \widehat {NMB} = \frac{{\widehat {ABC}}}{2} + \widehat {NMB}$ (do $BO$ là phân giác $\widehat {ABC}$ nên $\widehat {ABM} = \frac{{\widehat {ABC}}}{2}$) $ \Rightarrow \widehat {NMB} = \widehat {ADE} - \frac{{\widehat B}}{2} = {90^0} - \frac{{\widehat {BAC} + \widehat {ABC}}}{2} = \frac{{\widehat {ACB}}}{2}$.

Mặt khác $\widehat {NCB} = \frac{{\widehat {ACB}}}{2}$ (do $CO$ là tia phân giác $\widehat {ACB}$).

Suy ra $\widehat {NMB} = \widehat {NCB}$, mà $M,C$ là hai đỉnh liên tiếp của tứ giác $BCMN$$ \Rightarrow $Tứ giác $BCMN$ nội tiếp (vì cùng thuộc một cung chứa góc).

c) $\Delta NMO$ và $\Delta BCO$ có $\widehat {NOM} = \widehat {BOC}$ (đối đỉnh); $\widehat {NMO} = \widehat {BCO}$ (cmt)

$ \Rightarrow \Delta NMO\~\Delta BCO$ (g.g) $ \Rightarrow \frac{{OM}}{{OC}} = \frac{{ON}}{{OB}} = \frac{{MN}}{{BC}}$.

Tương tự (g.g) $ \Rightarrow \frac{{DM}}{{AC}} = \frac{{OM}}{{OC}}$;

$\Delta NEO\~\Delta BAO$ (g.g) $ \Rightarrow \frac{{NE}}{{AB}} = \frac{{ON}}{{OB}}$.

Vậy $\frac{{MN}}{{BC}} = \frac{{DM}}{{AC}} = \frac{{EN}}{{AB}}$.

Câu 9/21