Trên các cạnh \(BC,CD\) của hình vuông \(ABCD\) ta lấy lần lượt các điểm \(M,N\) sao cho \(\widehat {MAN} = {45^0}\). Đường thẳng \(BD\) cắt các đường thẳng \(AM,AN\) tương ứng tại các điểm \(P,Q\).
a) Chứng minh rằng các tứ giác \(ABMQ\) và \(ADNP\) nội tiếp.
b) Chứng minh rằng các điểm \(M,N,Q,P,C\) nằm trên cùng một đường tròn.
Trên các cạnh \(BC,CD\) của hình vuông \(ABCD\) ta lấy lần lượt các điểm \(M,N\) sao cho \(\widehat {MAN} = {45^0}\). Đường thẳng \(BD\) cắt các đường thẳng \(AM,AN\) tương ứng tại các điểm \(P,Q\).
a) Chứng minh rằng các tứ giác \(ABMQ\) và \(ADNP\) nội tiếp.
b) Chứng minh rằng các điểm \(M,N,Q,P,C\) nằm trên cùng một đường tròn.
Quảng cáo
Trả lời:
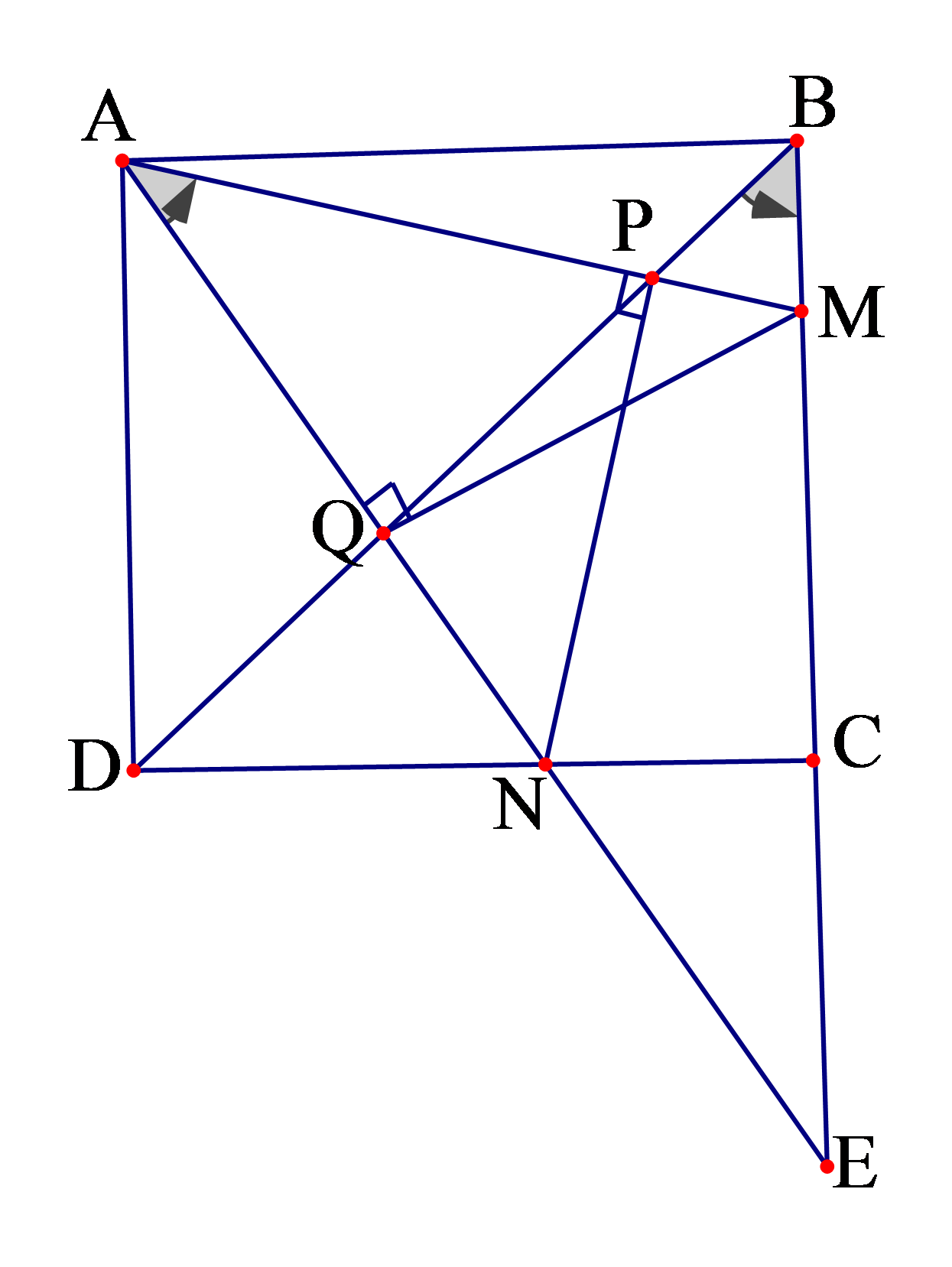
a). Gọi \(E\) là giao điểm của \(AN\) và \(BC\).
Các điểm \(M\) và \(Q\) nằm trên hai cạnh\(EB\) và \(EA\) của tam giác \(EBA\), nên tứ giác\(ABMQ\) là lồi. Các đỉnh \(A\) và \(B\) cùng nhìn đoạn thẳng \(MQ\) dưới một góc \({45^0}\) không đổi. Vì vậy tứ giác \(ABMQ\) nội tiếp.
Lập luận tương tự ta suy ra tứ giác \(ADNP\) nội tiếp.
b) Từ kết quả câu a, suy ra \(\widehat {ADP} = \widehat {ANP} = {45^0},\widehat {QAM} = \widehat {QBM} = {45^0}\)\( \Rightarrow NP \bot AM,MQ \bot AN\). Tập hợp các điểm \(P,Q,C\) nhìn đoạn \(MN\) dưới một góc vuông, nên các điểm này nằm trên đường tròn đường kính \(MN\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
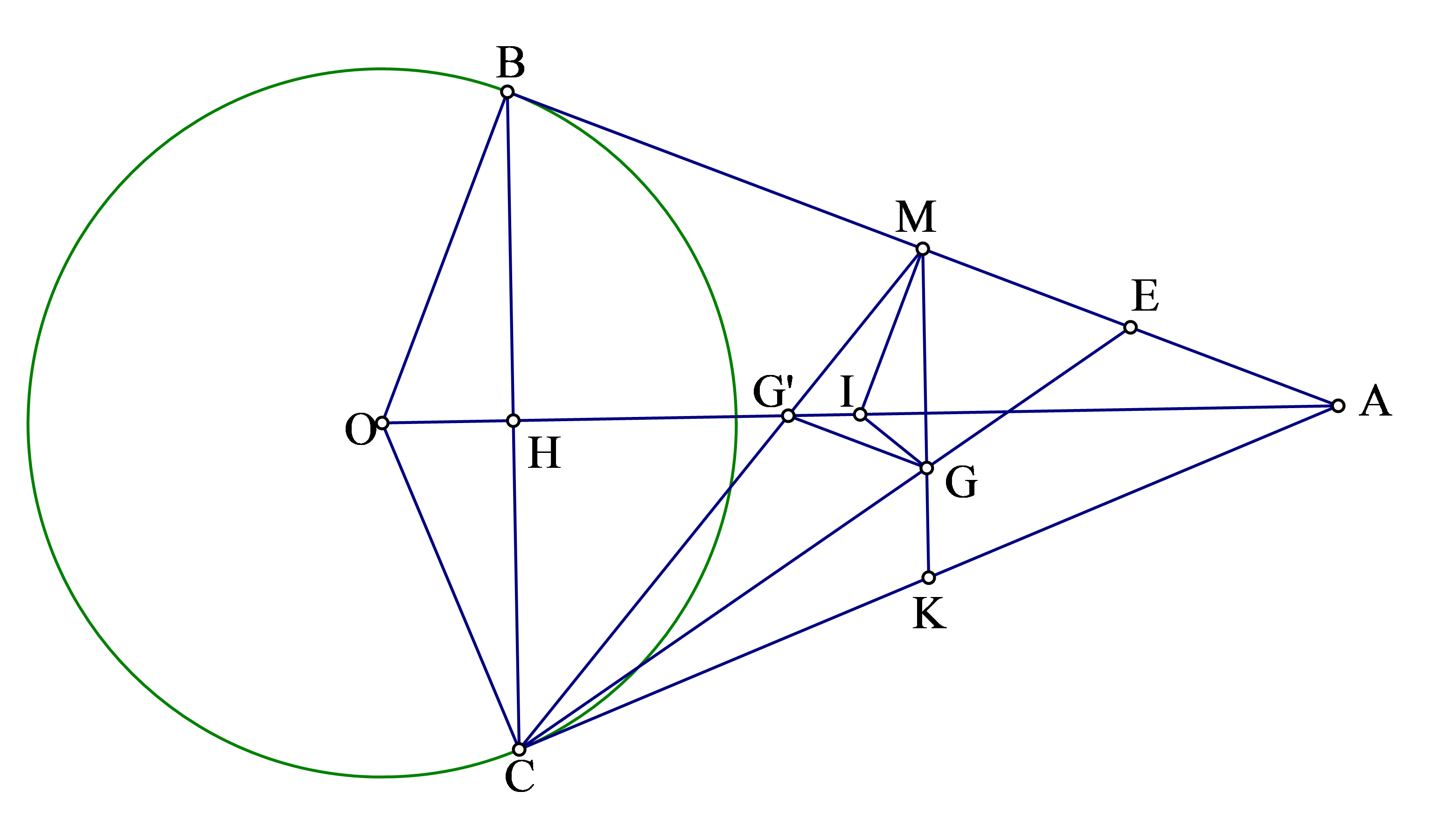
a) Do \(AB,AC\) là hai tiếp tuyến cắt nhau của đường tròn \(\left( O \right)\) nên \(\widehat {ABO} = \widehat {ACO} = {90^0} \Rightarrow B,C\) thuộc đường tròn đường kính \(OA\) có tâm \(I\) là trung điểm \(OA\).
b) Ta có \(AM.AO = \frac{{AB}}{2}.2AI = AB.AI\).
c) Gọi \(E\) là trung điểm \(MA\), do \(G\) là trọng tâm \(\Delta CMA\) nên \(G \in CE\) và \(\frac{{GE}}{{CE}} = \frac{1}{3}\).
Mặt khác \(\frac{{ME}}{{BE}} = \frac{1}{3}\) (vì \(ME = \frac{{MA}}{2} = \frac{{MB}}{2}\) nên \(ME = \frac{{BE}}{3}\)) \( \Rightarrow \frac{{GE}}{{CE}} = \frac{{ME}}{{BE}}\), theo định lý Ta-lét đảo \( \Rightarrow MG//BC\).
d) Gọi \(G'\) là giao điểm của \(OA\) và \(CM \Rightarrow G'\) là trọng tâm \(\Delta ABC\). Nên \(\frac{{G'M}}{{CM}} = \frac{1}{3} = \frac{{GE}}{{CE'}}\), theo định lý Ta-lét đảo \(GG'//ME\) (1)
\(MI\) là đường trung bình trong \(\Delta OAB \Rightarrow MI//OB\), mà \(AB \bot OB\) (cmt) \( \Rightarrow MI \bot AB\), nghĩa là \(MI \bot ME\) (2).
Từ (1) và (2) cho \(MI \bot GG'\), ta lại có \(GI' \bot MK\) (vì \(OA \bot MK\)) nên \(I\) là trực tâm \(\Delta MGG'\)\( \Rightarrow GI \bot G'M\) tức \(GI \bot CM\).
Lời giải
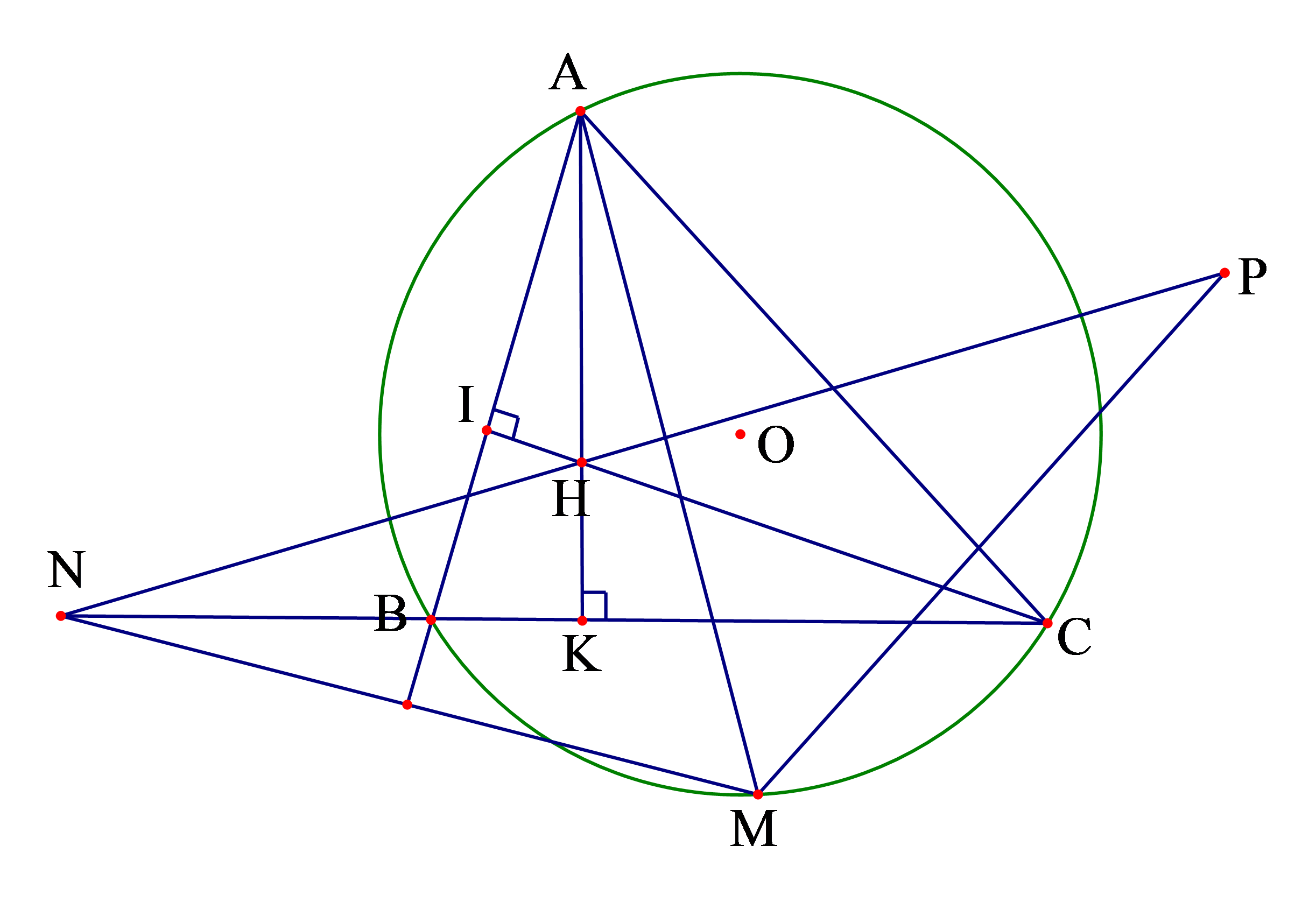
a). Giả sử các đường cao của tam giác là \(AK,CI\) . Để chứng minh \(AHCP\) là tứ giác nội tiếp ta sẽ chứng minh \(\widehat {AHC} + \widehat {APC} = {180^0}\).
Ta có:
\(\widehat {AHC} = \widehat {IHK}\) ( đối đỉnh)
\(\widehat {APC} = \widehat {AMC} = \widehat {ABC}\) ( do tính đối xứng và góc nội tiếp cùng chắn một cung).
Như vậy ta chỉ cần chứng minh \(\widehat {ABC} + \widehat {IHK} = {180^0}\) nhưng điều này là hiển nhiên do tứ giác \(BIHK\)là tứ giác nội tiếp.
b). Để chứng minh \(N,H,P\) thẳng hàng ta sẽ chứng minh \(\widehat {NHA} + \widehat {AHP} = {180^0}\) do đó ta sẽ tìm cách quy hai góc này về 2 góc đối nhau trong một tứ giác nội tiếp.
Thật vậy ta có: \(\widehat {AHP} = \widehat {ACP}\) (tính chất góc nội tiếp), \(\widehat {ACP} = \widehat {ACM}\) (1) (Tính chất đối xứng) .
Ta thấy vai trò tứ giác \(AHCP\) giống với \(AHBN\) nên ta cũng dễ chứng minh được \(AHBN\) là tứ giác nội tiếp từ đó suy ra \(\widehat {AHN} = \widehat {ABN}\) , mặt khác \(\widehat {ABN} = \widehat {ABM}\) (2) (Tính chất đối xứng) .
Từ (1), (2) ta suy ra chỉ cần chứng minh \(\widehat {ABM} + \widehat {ACM} = {180^0}\) nhưng điều này là hiển nhiên do tứ giác \(ABMC\) nội tiếp.
Vậy \(\widehat {NHA} + \widehat {AHP} = {180^0}\) hay \(N,H,P\) thẳng hàng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.