15 bài tập Toán 9 Kết nối tri thức Ôn tập chương 9 có đáp án

4.6 0 lượt thi 15 câu hỏi 45 phút

Câu 1

Tìm và gọi tên các đa giác đều trong hình dưới đây

Xem đáp án

Lời giải

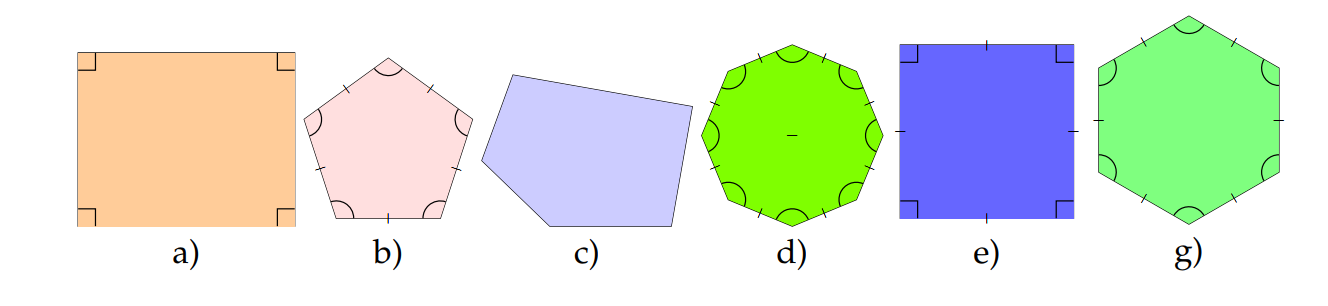
Hình b: Ngũ giác đều

Hình d: Bát giác đều

Hình e: Hình vuông.

Hình g: Ngũ giác đều

Câu 2

Tính số cạnh của một đa giác đều, biết mỗi góc của nó bằng \[135^\circ \].

Xem đáp án

Lời giải

Gọi \[n\] là số cạnh của đa giác đều.

Ta có \[\frac{{\left( {n - 2} \right).180^\circ }}{n} = 135^\circ \]

nên \[\frac{{n - 2}}{n} = \frac{{135}}{{180}} = \frac{3}{4}\].

Do đó \[4\left( {n - 2} \right) = 3n\].

Vậy \[n = 8\].

Câu 3

a) Tính số đường chéo của đa giác \[n\] cạnh.

b) Đa giác nào có số đường chéo bằng số cạnh?

Xem đáp án

Lời giải

a) Từ mỗi đỉnh của hình n – giác lồi. kẻ được \[n - 1\] đoạn thẳng đến các đỉnh còn lại, trong đó có hai đoạn thẳng là cạnh của đa giác, \[n - 3\] đoạn thẳng là đường chéo.

Đa giác có \[n\] đỉnh nên kẻ được \[n\left( {n - 3} \right)\] đường chéo, trong đó mỗi đường chéo tính 2 lần. Vậy số đường chéo của hình \[n\]- giác lồi là \[\frac{{n\left( {n - 3} \right)}}{2}\].

b) Giải phương trình \[\frac{{n\left( {n - 3} \right)}}{2} = n\]. Ta được \[n = 5\]

Câu 4

Cho tam giác $ABC$ vuông tại $A$. Trên $AC$ lấy một điểm $M$ và dựng đường tròn đường kính $MC$. Nối $BM$ kéo dài gặp đường tròn tại $D$. Đường thẳng $DA$ gặp đường tròn tại $S$. Chứng minh rằng $CA$ là tia phân giác của góc $\widehat {SCB}$.

Xem đáp án

Lời giải

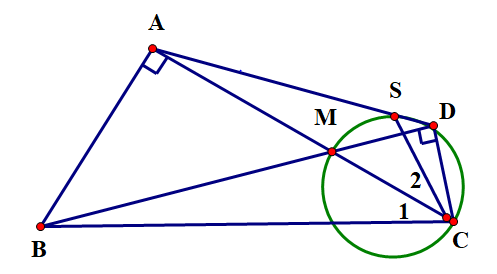
$Cho tam giác $ABC$ vuông tại $A$. (ảnh 1)$

Trường hợp 1: D nằm trên cung lớn .

Ta có $\widehat {{\rm{SCM}}} = \widehat {{\rm{SDM}}}$ (1) góc nội tiếp cùng chắn cung của đường tròn đường kính $MC$).

Dễ thấy $\hat{M D C} = 90^{°}$ (MC là đường kính). Tương tự $\hat{B A C} = 90^{°}$ (gt).

$ \Rightarrow $ Bốn điểm $B,A,D,C$ cùng nằm trên một đường tròn đường kính $BC$.

$ \Rightarrow \widehat {SDM} = \widehat {ACB}$ (2) (góc nội tiếp cùng chắn cung ).

Từ (1) và (2) $ \Rightarrow \widehat {SCM} = \widehat {MCB}$ hay $CA$ là tia phân giác của góc$SCB$.

Trường hợp 2: D nằm trên cung nhỏ và Trường hợp $3:{\rm{D}}$ trùng với S. (Học sinh tự giải).

Câu 5

$M$ ở chính giữa nửa đường tròn tâm $O$ đường kính $AB$. Trên cung nhỏ lấy điểm $C$ bất kì. Vẽ tiếp tuyến tại $B$ của $\left( O \right)$ cắt $MC$ tại $D$. Gọi $H$ là giao điểm của $MB$ và $AC$. Kẻ $HI$ vuông góc với $AB$. Chứng minh rằng $CA$ là tia phân giác của góc $\widehat {MCI}$.

Xem đáp án

Lời giải

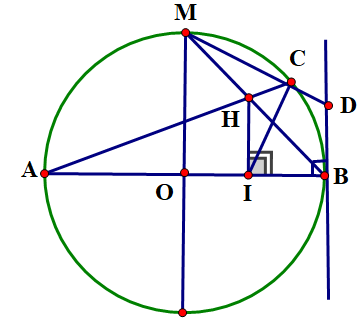
$$M$ ở chính giữa nửa đường tròn tâm $O$ đường (ảnh 1)$

Dễ thấy $\hat{ACB} = 90^{°}$ (vì $AB$ là đường kính); $\hat{HCB} = 90^{°}$ hay $C$ thuộc đường tròn đường kính $HB$.

Lại có $\hat{HIB} = 90^{°}$ (gt) nên $I$ thuộc đường tròn đường kính $HB$ nên bốn điểm $C,H,I,B$ cùng thuộc đường tròn đường kính $HB$. $ \Rightarrow \widehat {{\rm{HCI}}} = \widehat {{\rm{HBI}}}$ (1) (góc nội tiếp cùng chắn cung ).

Lại có $\widehat {{\rm{HBI}}} = \widehat {{\rm{MCA}}}$ (góc nội tiếp cùng chắn cung $MA$) $ \Rightarrow \widehat {{\rm{MCA}}} = \widehat {{\rm{MBA}}}$, chứng tỏ $CA$ là tia phân giác của góc $\widehat {{\rm{MCI}}}$.

Câu 6