12 bài tập Các bài toán liên quan đến hai đường tròn tiếp xúc nhau, cắt nhau và không cắt nhau có lời giải
32 người thi tuần này 4.6 491 lượt thi 12 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
20 bài tập Toán 9 Cánh diều Bài 2. Hình nón có đáp án
Danh sách câu hỏi:
Câu 1
A. OD ∕∕ O'C.
B. \(\frac{{AD}}{{AC}} = \frac{1}{2}\).
C. \(\frac{{AD}}{{AC}} = 3\).
D. AD = AC.
Lời giải
Đáp án đúng là: C
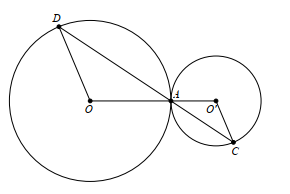
Xét đường tròn (O') và (O) có O'A = \(\frac{1}{2}\)OA nên \(\frac{{AO}}{{AO'}} = 2\).
Xét ∆O'AC cân tại O' và ∆OAD cân tại D có \(\widehat {OAD} = \widehat {O'AD}\) (đối đỉnh) nên \(\widehat {OAD} = \widehat {O'CA}\).
Suy ra \(\widehat {OAD} = \widehat {O'AD}\).
Suy ra ∆OAD ∽ ∆O'AD (g.g) suy ra \(\frac{{AD}}{{AC}} = \frac{{AO}}{{AO'}} = 2\).
Lại có \(\widehat {OAD} = \widehat {O'CA}\) mà hai góc ở vị trí so le trong nên OD ∕∕ O'C.
Câu 2
A. 7 cm.
B. 1 cm.
D. 17 cm.
D. \(\frac{7}{2}\) cm.
Lời giải
Đáp án đúng là: A

Kẻ O'H ⊥ OM và OK ⊥ O'F.
Ta có: OH = R – r; O'K = R + r.
Mà OH2 = O'O2 – MN2; O'K2 = O'O2 – EF2 = 64.
Suy ra OH = 6 và O'K = 8.
Suy ra R – r = 6 và R + r = 8.
Thay R = r + 6 vào R + r = 8 được 2r + 6 = 8 suy ra r = 1.
Do đó R = 7 cm.
Vậy chọn A.
Câu 3
A. 7 cm.
B. 1 cm.
D. \(\frac{{17}}{2}\) cm.
D. \(\frac{7}{2}\) cm.
Lời giải
Đáp án đúng là: D

Kẻ O'H ⊥ OM và OK ⊥ O'F.
Ta có: OH = R – r; O'K = R + r.
Mà OH2 = O'O2 – MN2 = 25; O'K2 = O'O2 – EF2 = 144.
Suy ra OH = 5 và O'K = 12.
Suy ra R – r = 5 và R + r = 12.
Thay R = r + 5 vào R + r = 12 được 2r + 5 = 12 suy ra r = \(\frac{7}{2}\).
Do đó R = \(\frac{{17}}{2}\) cm.
Vậy chọn D.
Câu 4
A. MP + NQ.
B. MQ + NP.
C. 2MP.
d. OP + PQ.
Lời giải
Đáp án đúng là: A
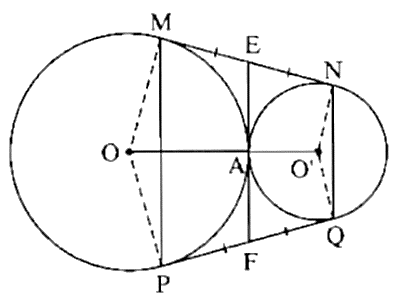
Vì P đối xứng với M qua OO', Q là điểm đối xứng với N qua OO' nên MN = QP; P ∈ (O) và Q ∈ (O').
Mà MP ⊥ OO'; NQ ⊥ OO' nên MP ∕∕ NQ mà \(\widehat {NMP} = \widehat {QPM}\) (do \(\widehat {OMN} = \widehat {OPQ};\widehat {OMP} = \widehat {OPM}\)).
Nên MNPQ là hình thang cân.
Có MN là tiếp tuysn chung nên MN ⊥ OM (tính chất) nên \(\widehat {OMN}\) = 90 ° hay \(\widehat {OMP} + \widehat {PMN} = 90^\circ \).
Ta có: OM = OP = R nên ∆OMP cân tại O.
Suy ra \(\widehat {OPM} = \widehat {OMP}\).
Lại có MNPQ là hình thang cân nên \(\widehat {PMN} = \widehat {QPM}\).
Từ đây suy ra \(\widehat {QPM} + \widehat {QPM} = 90^\circ \). Suy ra QP ⊥ OP tại P.
Kẻ tiếp tuyến chung tại A cắt NM tại E và PQ tại F.
Trong đường tròn (O), theo tính chất hai tiếp tuyến cắt nhau, ta có: EM = EA và FP = FA.
Trong đường tròn (O'), theo tính chất hai tiếp tuyến bằng nhau ta có:
EN = EA và FQ = FA.
Suy ra EM = EA = EN = \(\frac{1}{2}MN\).
FP = FA = FQ = \(\frac{1}{2}PQ\).
Suy ra MN + PQ = 2EA + 2FA = 2(EA + FA) = 2EF.
Vì EF là đường trung bình của hình thang MNPQ nên
EF = \(\frac{{MP + NQ}}{2}\) hay MP + NQ = 2EF.
Do đó, MN + PQ = MP + NQ.
Câu 5
A. Hình thang cân.
B. Hình thang.
C. Hình thang vuông.
D. Hình bình hành.
Lời giải
Đáp án đúng là: A
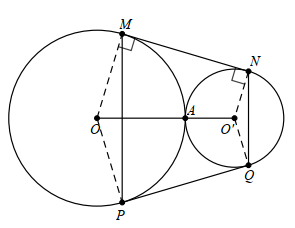
Vì P đối xứng với M qua OO', Q là điểm đối xứng với N qua OO' nên MN = QP; P ∈ (O) và Q ∈ (O').
Mà MP ⊥ OO'; NQ ⊥ OO' nên MP ∕∕ NQ mà \(\widehat {NMP} = \widehat {QPM}\)
(do \(\widehat {OMN} = \widehat {OPQ};\widehat {OMP} = \widehat {OPM}\)).
Nên MNPQ là hình thang cân.
Câu 6
A. AC = CB.
B. \(\widehat {CBO'} = 90^\circ \).
C. CA, CB là hai tiếp tuyến của (O').
D. CA, CB là hai cát tuyến của (O').
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(AB = \frac{{60}}{{13}}\) cm.
B. \(AB = \frac{{120}}{{13}}\) cm.
C. AB = 10 cm.
D. AB = 5 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. 12 cm2.
B. 24 cm2.
C. 48 cm2.
D. 36 cm2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 1
Sử dụng dữ kiện của bài toán dưới đây để trả lời Bài 7, 8.
Cho hai đường tròn (O; R) và (O'; r) (R > r) tiếp xúc ngoài tại A. Vẽ các bán kính OB ∕∕ O'D với B, D ở cùng phía nửa mặt phẳng bờ OO'. Đường thẳng BD và OO' cắt nhau tại I. Tiếp tuyến chung ngoài GH của (O) và (O') với G, H nằm ở nửa mặt phẳng bờ OO' không chứa B, D.
Câu 11
A. \(OI = \frac{{R + r}}{{R - r}}\).
B. \(OI = \frac{{R - r}}{{R + r}}\).
C. \(OI = \frac{{R\left( {R - r} \right)}}{{R + r}}\).
D. \(OI = \frac{{R\left( {R + r} \right)}}{{R - r}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. BD, OO' và GH đồng quy.
B. BD, OO' và GH không đồng quy.
C. Không có ba đường nào đồng quy.
D. Cả A, B, C đều sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.