Cho đoạn OO' và điểm A nằm trên đoạn OO' sao cho OA = 2O'A. Đường tròn (O) bán kính OA và đường tròn (O') bán kính O'A. Dây AD của đường tròn lớn cắt đường tròn nhỏ tại C. Khi đó:
A. OD ∕∕ O'C.
B. \(\frac{{AD}}{{AC}} = \frac{1}{2}\).
C. \(\frac{{AD}}{{AC}} = 3\).
D. AD = AC.
Quảng cáo
Trả lời:
Đáp án đúng là: C
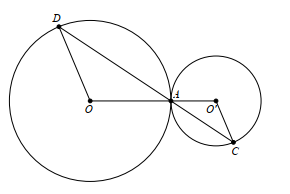
Xét đường tròn (O') và (O) có O'A = \(\frac{1}{2}\)OA nên \(\frac{{AO}}{{AO'}} = 2\).
Xét ∆O'AC cân tại O' và ∆OAD cân tại D có \(\widehat {OAD} = \widehat {O'AD}\) (đối đỉnh) nên \(\widehat {OAD} = \widehat {O'CA}\).
Suy ra \(\widehat {OAD} = \widehat {O'AD}\).
Suy ra ∆OAD ∽ ∆O'AD (g.g) suy ra \(\frac{{AD}}{{AC}} = \frac{{AO}}{{AO'}} = 2\).
Lại có \(\widehat {OAD} = \widehat {O'CA}\) mà hai góc ở vị trí so le trong nên OD ∕∕ O'C.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 12 cm2.
B. 24 cm2.
C. 48 cm2.
D. 36 cm2.
Lời giải
Đáp án đúng là: B
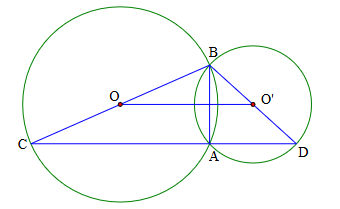
∆BCD có OO' là đường trung bình suy ra OO' ∕∕ CD.
∆ABC có OI là đường trung bình suy ra OO' ∕∕ CA.
Do đó A, C, D thẳng hàng.
Ta có: ∆BOO' vuông tại B suy ra ∆BCD vuông tại B.
Do đó diện tích tam giác BCD là: S = \(\frac{1}{2}BC.BD = \frac{1}{2}.6.8 = 24\) cm2.
Câu 2
A. MP + NQ.
B. MQ + NP.
C. 2MP.
d. OP + PQ.
Lời giải
Đáp án đúng là: A
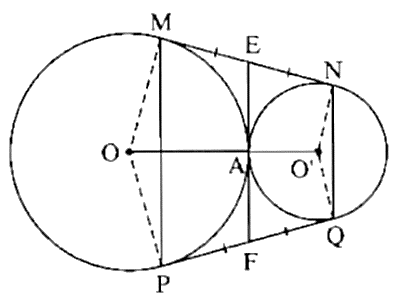
Vì P đối xứng với M qua OO', Q là điểm đối xứng với N qua OO' nên MN = QP; P ∈ (O) và Q ∈ (O').
Mà MP ⊥ OO'; NQ ⊥ OO' nên MP ∕∕ NQ mà \(\widehat {NMP} = \widehat {QPM}\) (do \(\widehat {OMN} = \widehat {OPQ};\widehat {OMP} = \widehat {OPM}\)).
Nên MNPQ là hình thang cân.
Có MN là tiếp tuysn chung nên MN ⊥ OM (tính chất) nên \(\widehat {OMN}\) = 90 ° hay \(\widehat {OMP} + \widehat {PMN} = 90^\circ \).
Ta có: OM = OP = R nên ∆OMP cân tại O.
Suy ra \(\widehat {OPM} = \widehat {OMP}\).
Lại có MNPQ là hình thang cân nên \(\widehat {PMN} = \widehat {QPM}\).
Từ đây suy ra \(\widehat {QPM} + \widehat {QPM} = 90^\circ \). Suy ra QP ⊥ OP tại P.
Kẻ tiếp tuyến chung tại A cắt NM tại E và PQ tại F.
Trong đường tròn (O), theo tính chất hai tiếp tuyến cắt nhau, ta có: EM = EA và FP = FA.
Trong đường tròn (O'), theo tính chất hai tiếp tuyến bằng nhau ta có:
EN = EA và FQ = FA.
Suy ra EM = EA = EN = \(\frac{1}{2}MN\).
FP = FA = FQ = \(\frac{1}{2}PQ\).
Suy ra MN + PQ = 2EA + 2FA = 2(EA + FA) = 2EF.
Vì EF là đường trung bình của hình thang MNPQ nên
EF = \(\frac{{MP + NQ}}{2}\) hay MP + NQ = 2EF.
Do đó, MN + PQ = MP + NQ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. AC = CB.
B. \(\widehat {CBO'} = 90^\circ \).
C. CA, CB là hai tiếp tuyến của (O').
D. CA, CB là hai cát tuyến của (O').
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. 7 cm.
B. 1 cm.
D. \(\frac{{17}}{2}\) cm.
D. \(\frac{7}{2}\) cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.