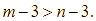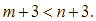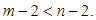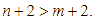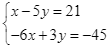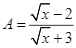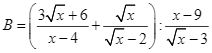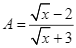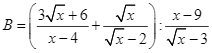Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 06
30 người thi tuần này 4.6 18.7 K lượt thi 19 câu hỏi 90 phút
🔥 Đề thi HOT:
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
30.6 K lượt thi
3 câu hỏi
123 bài tập Nón trụ cầu và hình khối có lời giải
3.2 K lượt thi
123 câu hỏi
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
3.9 K lượt thi
16 câu hỏi
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
7.1 K lượt thi
5 câu hỏi
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
26.5 K lượt thi
4 câu hỏi
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
19.1 K lượt thi
20 câu hỏi
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
6.2 K lượt thi
87 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
Đáp án đúng là: B
Thực hiện xét các đáp án, ta có:
Thay 
vào phương trình 
, ta được: 
Do đó, 
không là nghiệm của phương trình .
Thay 
vào phương trình , ta được: 
.
Do đó, 
là nghiệm của phương trình .
Thay 
vào phương trình , ta được: 
.
Do đó, 
không là nghiệm của phương trình .
Thay 
vào phương trình , ta được: 
.
Do đó 
không là nghiệm của phương trình .
Vậy cặp số là nghiệm của phương trình .
Lời giải
Đáp án đúng là: A
Trừ hai vế của bất đẳng thức 
cho 3, ta được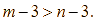 
Lời giải
Đáp án đúng là: B
|
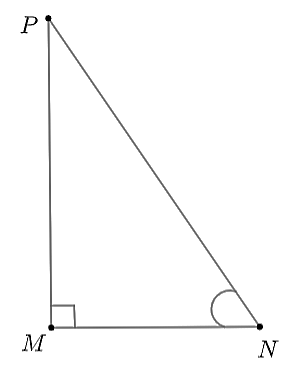
Xét tam giác |
|
Lời giải
Đáp án đúng là: D
Góc ở tâm là góc có đỉnh trùng với tâm đường tròn.
Lời giải
Đáp án: a) S b) Đ c) Đ d) S
a) Ta có 
hay 
nên 
.
Khi đó 
hoặc 
.
Do đó 
hoặc 
Vậy khi thì hoặc
b) Để biểu thức 
có nghĩa thì 
.
Vì 
với mọi 
nên để thì 
.
Vậy để biểu thức có nghĩa thì và 
c) Với 
(TMĐK) thì
Vậy với thì giá trị của biểu thức là 2.
d) Ta 
(vì 
với mọi ).
Vậy 
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
4.6
3734 Đánh giá
50%
40%
0%
0%
0%