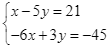Cho đường tròn 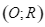 , đường kính
, đường kính 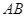 . Qua
. Qua 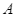 và
và 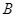 vẽ lần lượt hai tiếp tuyến
vẽ lần lượt hai tiếp tuyến 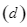 và
và 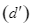 với đường tròn
với đường tròn 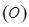 . Một đường thẳng
. Một đường thẳng 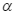 qua
qua 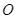 cắt đường thẳng
cắt đường thẳng 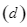 ở
ở 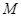 và cắt đường thẳng
và cắt đường thẳng 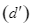 ở
ở 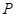 . Từ
. Từ 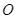 vẽ một tia vuông góc với
vẽ một tia vuông góc với  và cắt đường thẳng
và cắt đường thẳng 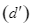 ở
ở 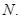 Đường thẳng
Đường thẳng 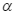 cắt đường tròn
cắt đường tròn 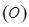 tại hai điểm
tại hai điểm 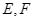 (
( nằm giữa
nằm giữa 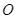 và
và 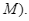 Cho
Cho 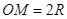 .
Gọi
.
Gọi 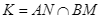 . Cho
. Cho 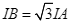 , tính diện tích tam giác
, tính diện tích tam giác 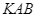 theo
theo 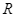 .
.
Quảng cáo
Trả lời:
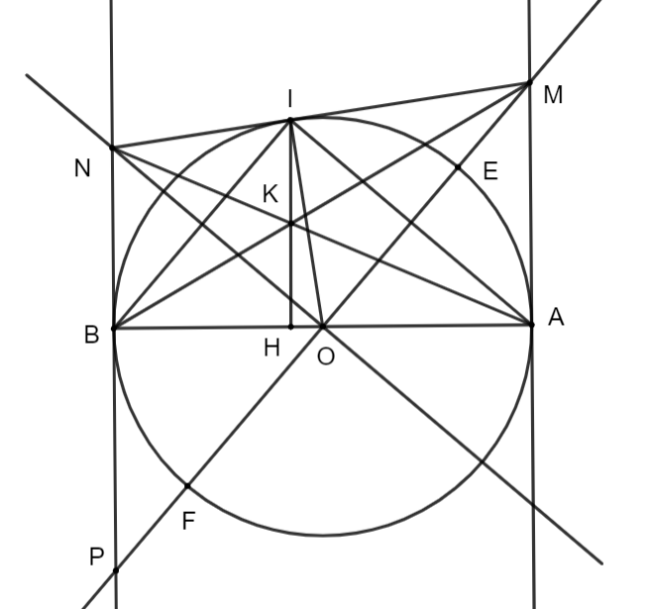
Ta có ![]() (cùng vuông với
(cùng vuông với ![]() ).
).
Xét ![]() và
và ![]() , có:
, có:
![]() (so le trong)
(so le trong)
![]() (đối đỉnh)
(đối đỉnh)
Do đó, ![]() (g.g). Suy ra
(g.g). Suy ra ![]() .
.
Mà, ta có: ![]() (tính chất hai tiếp tuyến cắt nhau).
(tính chất hai tiếp tuyến cắt nhau).
Suy ra ![]() .
.
Xét tam giác ![]() , có:
, có: ![]() nên
nên ![]() (Thalès đảo).
(Thalès đảo).
Mà ![]() nên
nên ![]() .
.
Kéo dài ![]() cắt
cắt ![]() tại
tại ![]() thì
thì ![]() .
.
Xét ![]() có:
có: ![]() nên theo định lý Thalès có:
nên theo định lý Thalès có: ![]() .
.
Xét ![]() có
có ![]() nên theo định lý Thalès có:
nên theo định lý Thalès có: ![]() .
.
Xét ![]() có
có ![]() nên theo định lý Thalès có:
nên theo định lý Thalès có: ![]() .
.
Suy ra ![]() , do đó
, do đó ![]() hay
hay ![]() là trung điểm của
là trung điểm của ![]() .
.
Xét ![]() và
và ![]() có chung đáy
có chung đáy ![]() và đường cao
và đường cao ![]()
Suy ra ![]() .
.
Áp dụng định lí Pythagore vào ![]() với
với ![]() , ta được:
, ta được:
![]()
![]()
![]()
![]()
Suy ra ![]() và
và ![]() .
.
Do đó ![]() (đvdt).
(đvdt).
Vậy diện tích tam giác ![]() là
là ![]() (đvdt).
(đvdt).
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
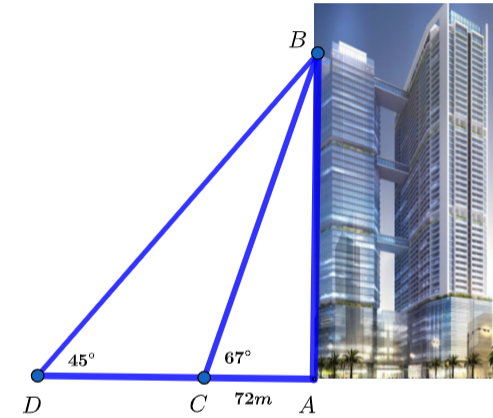
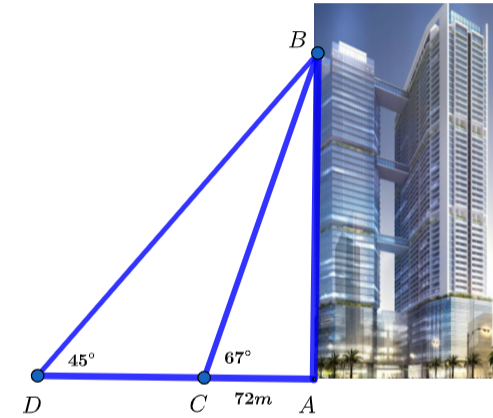
Chiều cao của tòa tháp chính là độ dài đoạn ![]() .
.
Xét tam giác vuông ![]() , ta có:
, ta có:
![]()
Vậy chiều cao của tòa tháp chung cư này là ![]() .
.
Lời giải
Gọi ![]() lần lượt là khối lượng táo và xoài mà bác Nam mua
lần lượt là khối lượng táo và xoài mà bác Nam mua ![]()
Theo đề bài, ta có phương trình về khối lượng về táo và xoài là ![]()
Tổng giá trị của thùng trái cây là ![]() đồng nên
đồng nên ![]()
Từ ![]() và
và ![]() ta có hệ phương trình
ta có hệ phương trình 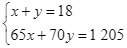
Từ phương trình thứ nhất của hệ, ta có: ![]() , thế vào phương trình thứ hai, ta được:
, thế vào phương trình thứ hai, ta được:
![]()
![]()
![]()
![]()
![]() (TMĐK).
(TMĐK).
Thay ![]() vào phương trình thứ nhất, ta được:
vào phương trình thứ nhất, ta được: ![]() (TMĐK).
(TMĐK).
Vậy bác Nam đã mua 11 kg táo và 7 kg xoài.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.