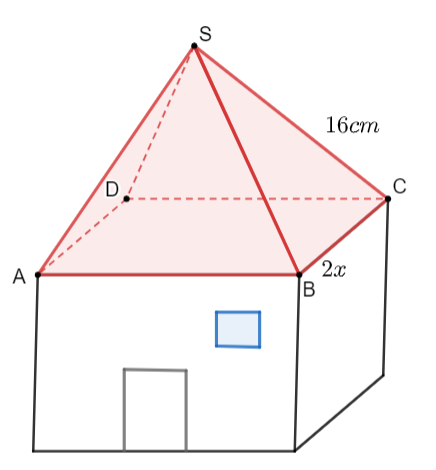
Bạn Nam làm một căn nhà đồ chơi bằng gỗ có phần mái là một chóp tứ giác đều. Biết các cạnh bên của mái nhà bạn Nam dùng các thanh gỗ có chiều dài 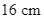 . Bạn Nam dự định dùng giấy màu để phủ kín phần mái nhà. Gọi độ dài cạnh đáy của phần mái là
. Bạn Nam dự định dùng giấy màu để phủ kín phần mái nhà. Gọi độ dài cạnh đáy của phần mái là 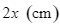 . Hỏi diện tích giấy màu cần sử dụng nhiều nhất là bao nhiêu?
. Hỏi diện tích giấy màu cần sử dụng nhiều nhất là bao nhiêu?

Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Diện tích giấy màu cần sử dụng chính bằng tổng diện tích bốn mặt bên là các tam giác cân có cạnh bên bằng ![]() và cạnh đáy là
và cạnh đáy là ![]() .
.
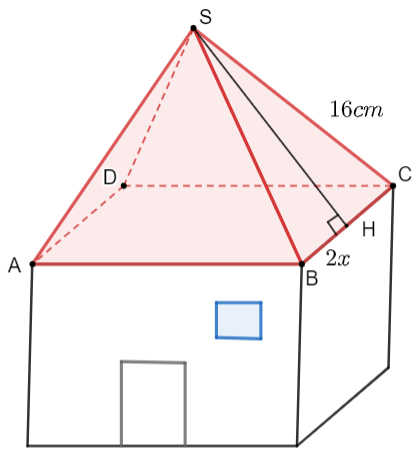
Xét tam giác ![]() , kẻ đường cao
, kẻ đường cao ![]() tại
tại ![]() .
.
Do tam giác ![]() cân tại
cân tại ![]() nên
nên ![]() vừa là đường cao, vừa là đường trung trực suy ra
vừa là đường cao, vừa là đường trung trực suy ra ![]() là trung điểm của
là trung điểm của ![]() .
.
Suy ra 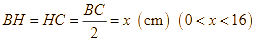 .
.
Áp dụng định lí Pythagore vào tam giác ![]() , ta có:
, ta có: ![]()
Suy ra ![]() .
.
Do đó ![]() .
.
Diện tích tam giác ![]() là
là ![]() .
.
Diện tích giấy màu cần sử dụng là ![]() .
.
Thực hiện tính giá trị lớn nhất của ![]() với
với ![]() .
.
Ta có: ![]()
![]()
![]() .
.
Vì ![]() với mọi
với mọi ![]() nên
nên ![]() với mọi
với mọi ![]() .
.
Suy ra ![]() với mọi
với mọi ![]() .
.
Do đó, ![]() với mọi
với mọi ![]() .
.
Dấu ![]() xảy ra khi
xảy ra khi ![]() hay
hay 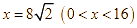 .
.
Vậy diện tích giấy màu cần sử dụng nhiều nhất là ![]() .
.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi ![]() (ngày) lần lượt là số ngày đội
(ngày) lần lượt là số ngày đội ![]() và đội
và đội ![]() làm một mình để hoàn thành công việc
làm một mình để hoàn thành công việc ![]() .
.
Trong một ngày đội ![]() làm được
làm được ![]() công việc, đội
công việc, đội ![]() làm được
làm được ![]() công việc.
công việc.
Trong một ngày, hai đội làm chung được số phần công việc là: ![]() (công việc).
(công việc).
Trong 8 ngày, số phần công việc hai đội làm được là: 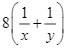 (công việc).
(công việc).
Sau 8 ngày, phần công việc còn lại là: 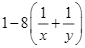 (công việc).
(công việc).
Theo đề bài, khi làm một mình đội ![]() tăng gấp đôi năng suất. Lúc này, trong 1 ngày, đội
tăng gấp đôi năng suất. Lúc này, trong 1 ngày, đội ![]() làm được:
làm được: ![]() (công việc).
(công việc).
Trong 8 ngày tiếp theo, đội ![]() đã hoàn thành phần việc còn lại, nên ta có phương trình:
đã hoàn thành phần việc còn lại, nên ta có phương trình:
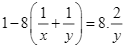 hay
hay ![]() .
.
Mà ban đầu hai đội dự định hoàn thành công việc trong 12 ngày khi làm chung. Do đó, ta có phương trình:
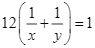 hay
hay ![]() .
.
Từ ![]() và
và ![]() , ta có hệ phương trình sau:
, ta có hệ phương trình sau: 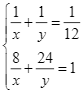 .
.
Từ phương trình thứ hai của hệ, ta có ![]() vào phương trình
vào phương trình ![]() , ta được:
, ta được:
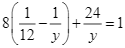 hay
hay ![]() suy ra
suy ra ![]() khi
khi ![]() (TMĐK).
(TMĐK).
Thay ![]() vào phương trình
vào phương trình ![]() suy ra
suy ra ![]() , suy ra
, suy ra ![]() (TMĐK).
(TMĐK).
Vậy đội ![]() làm một mình sẽ hoàn thành công việc trong
làm một mình sẽ hoàn thành công việc trong ![]() ngày, đội
ngày, đội ![]() làm một mình sẽ hoàn thành công việc trong
làm một mình sẽ hoàn thành công việc trong ![]() ngày.
ngày.
Câu 2
|
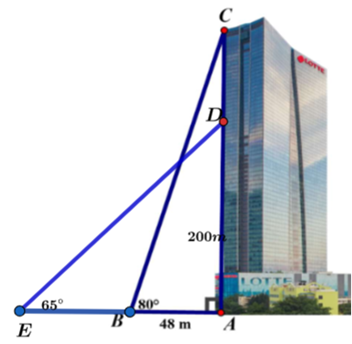
(1,0 điểm) Một người có tầm mắt cao \[1,65{\rm{ m}}\] đứng trên tầng thượng của tòa Lotte Center thì nhìn thấy một chiếc xe thu gom phế thải đang dừng ở \[B\] với góc nghiêng \[80^\circ \] (như hình vẽ). Biết xe đó cách tòa nhà \(48{\rm{ m}}\). a) Tính chiều cao của tòa nhà Lotte Center. b) Một người ở độ cao \[200{\rm{ m}}\] của tòa nhà cũng nhìn thấy xe thu gom phế thải khác đang dừng ở \[E\] với góc nghiêng \(65^\circ \). Hỏi hai xe thu gom phế thải cách nhau bao nhiêu mét? (tất cả các kết quả làm tròn đến hàng phần trăm) |
 |
Lời giải
a) Từ hình vẽ, ta xét tam giác vuông \(ABC\), có:
\(AC = AB.\tan \widehat {CBA} = 48.\tan 80^\circ \approx 272,22{\rm{ }}\left( {\rm{m}} \right){\rm{.}}\)
Do người đó có tầm mắt \[1,65{\rm{ m}}\] nên chiều cao của tòa nhà là:
\[272,22 - 1,65 = 270,57{\rm{ }}\left( {\rm{m}} \right)\].
Vậy tòa nhà Lotte Center cao \[270,57{\rm{ m}}\].
b) Khoảng cách từ xe thu gom phế thải ở \[E\] đến chân tòa nhà là độ dài đoạn \[EA\].
Xét tam giác vuông \[EAD\], ta có:
\[EA = \frac{{AD}}{{\tan \widehat {DEA}}} = \frac{{200}}{{\tan 65^\circ }} \approx 93,26{\rm{ }}\left( {\rm{m}} \right){\rm{.}}\]
Khoảng cách của hai xe phế thải là: \[93,26 - 48 = 45,26{\rm{ }}\left( {\rm{m}} \right){\rm{.}}\]
Vậy hai xe phế thải cách nhau \[45,26{\rm{ m}}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.