Sau khi thực hiện các bước giải hệ phương trình \(\left\{ \begin{array}{l}2x + y = 1\\ - 4x - 2y = - 2\end{array} \right.\) theo phương pháp cộng đại số, bạn An được phương trình \(0x = 0.\) Bạn An cần viết kết luận về nghiệm của hệ phương trình như nào? 

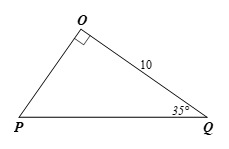
a) Xét tam giác \(OPQ\) vuông tại \(O\), ta có:

⦁ \(OQ = OQ \cdot \tan Q = 10 \cdot \tan 35^\circ  \approx 7,00{\rm{\;(cm}});\)

⦁ \(OQ = PQ \cdot \cos Q\)

Suy ra \(PQ = \frac{{OQ}}{{\cos Q}} = \frac{{10}}{{\cos 35^\circ }} \approx 12,21{\rm{\;(cm)}}{\rm{.}}\)

Vậy \(OQ \approx 7,00{\rm{\;cm}},\,\,PQ \approx 12,21{\rm{\;cm}}.\)

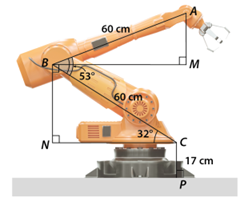
b) Xét \(\Delta BCN\) vuông tại \(N,\) ta có:

\(BN = BC \cdot \sin \widehat {BCN} = 60 \cdot \sin 32^\circ  \approx 31,80{\rm{\;(cm)}}{\rm{.}}\)

Ta thấy \(NC\) và \(BM\) là các đoạn thẳng nằm trên phương ngang nên \(NC\,{\rm{//}}\,BM,\) suy ra \(\widehat {CBM} = \widehat {BCN} = 32^\circ \) (so le trong).

Khi đó, \(\widehat {ABM} = \widehat {ABC} - \widehat {CBM} = 53^\circ  - 32^\circ  = 21^\circ \).

Xét \(\Delta ABM\) vuông tại \(M\), ta có:

\(AM = AB \cdot \sin \widehat {ABM} = 60 \cdot \sin 21^\circ  \approx 21,50\) (cm).

Vậy, độ cao của điểm \(A\) trên đầu cánh tay robot so với mặt đất là:

\(AM + BN + CP \approx 21,50 + 31,80 + 17 = 70,3\) (cm).

a) Vì số nguyên tử của \({\rm{Fe}}\) và \({\rm{O}}\) ở cả hai vế của phương trình phản ứng phải bằng nhau nên ta có hệ phương trình: \(\left\{ \begin{array}{l}x = 2 \cdot 3\\x + 2y = 2 \cdot 4\end{array} \right.\) hay \(\left\{ \begin{array}{l}x = 6\\x + 2y = 8.\end{array} \right.\)

Thay \(x = 6\) vào phương trình \(x + 2y = 8,\) ta được:

\(6 + 2y = 8,\) suy ra \(2y = 2,\) nên \(y = 1.\)

Vậy \(x = 6\) và \(y = 1.\) Khi đó ta hoàn thiện phương trình phản ứng hóa học sau cân bằng như sau:

\({\rm{6FeO}} + {{\rm{O}}_2}\mathop \to \limits^{{\rm{t}}^\circ } 2{\rm{F}}{{\rm{e}}_3}{{\rm{O}}_4}.\)

b) Gọi \(x\) (đồng) và \(y\) (đồng) lần lượt là giá vé cáp treo khứ hồi và giá vé 1 lượt \(\left( {x > 0,\,\,y > 0} \right).\)

Do giá vé 1 lượt rẻ hơn giá vé khứ hồi là \[70{\rm{ }}000\] đồng nên ta có phương trình:

\(x - y = 70\,\,000.\,\,\,\left( 1 \right)\)

Do trong đoàn \(40\) người chỉ có \(5\) người mua vé cáp treo \(1\) lượt cho lượt xuống nên đã có \(40 - 5 = 35\) người mua vé cáp treo khứ hồi.

Khi đó, số tiền cần trả để mua \(35\) vé cáp treo khứ hồi và \(5\) vé cáp treo 1 lượt là: \(35x + 5y\) (đồng).

Theo bài, cả đoàn khách du lịch này đã chi ra \[8{\rm{ }}450{\rm{ }}000\] đồng để mua vé nên ta có phương trình:

\(35x + 5y = 8{\rm{ }}450{\rm{ }}000.\,\,\,\left( 2 \right)\)

Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta có hệ phương trình: \(\left\{ \begin{array}{l}x - y = 70\,\,000\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\35x + 5y = 8{\rm{ }}450{\rm{ }}000\,\,\,\,\left( 2 \right)\end{array} \right.\)

Nhân hai vế của phương trình \(\left( 1 \right)\) với \(5,\) ta được hệ phương trình mới là: \(\left\{ \begin{array}{l}5x - 5y = 350\,\,000\\35x + 5y = 8{\rm{ }}450{\rm{ }}000.\end{array} \right.\)

Cộng từng vế hai phương trình của hệ phương trình trên, ta được:

\(40x = 8\,\,800\,\,000,\) suy ra \(x = 220\,\,000\) (thỏa mãn).

Thay \(x = 220\,\,000\) vào phương trình \(\left( 1 \right),\) ta được:

\(220\,\,000 - y = 70\,\,000,\) suy ra \(y = 150\,\,000\) (thỏa mãn).

Do đó hệ phương trình trên có nghiệm là \(\left( {x;\,\,y} \right) = \left( {220\,\,000;\,\,150\,\,000} \right).\)

Vậy giá vé cáp treo khứ hồi và giá vé cáp treo 1 lượt lần lượt là \(200\,\,000\) đồng và \(150\,\,000\) đồng.