Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 12 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: D
Ta có:
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{x - 2}}{{x + 2}} = 1.\)
\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{x - 2}}{{x + 2}} = 1.\)
Do đó, \(y = 1\) là đường tiệm cận ngang của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to - {2^ - }} y = \mathop {\lim }\limits_{x \to - {2^ - }} \frac{{x - 2}}{{x + 2}} = + \infty .\)
\(\mathop {\lim }\limits_{x \to - {2^ + }} y = \mathop {\lim }\limits_{x \to - {2^ + }} \frac{{x - 2}}{{x + 2}} = - \infty .\)
Do đó, \(x = - 2\) là đường tiệm cận đứng của đồ thị hàm số.
Vậy tọa độ giao điểm \(I\) của hai đường tiệm cận của đồ thị \[\left( C \right)\] là \(I\left( { - 2;1} \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Xét: \(h(t) = - \frac{1}{3}{t^3} + 5{t^2} + 24t\), \(\left( {t > 0} \right).\)
Ta có: \(h'(t) = - {t^2} + 10t + 24\)
\(h'(t) = 0 \Leftrightarrow - {t^2} + 10t + 24 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 12 \in \left( {0; + \infty } \right)\\t = - 2 \notin \left( {0; + \infty } \right)\end{array} \right.\)
Bảng biến thiên:
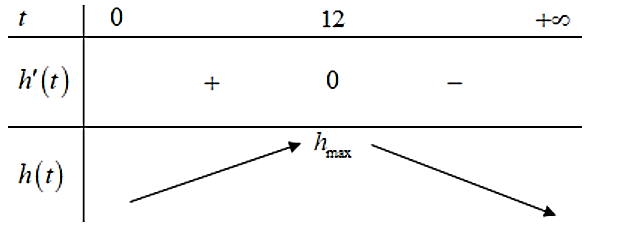
Để mực nước lên cao nhất thì phải mất 12 giờ.
Vậy phải thông báo cho dân dời đi vào 15 giờ chiều cùng ngày.
Câu 2
Lời giải
Đáp án đúng là: A
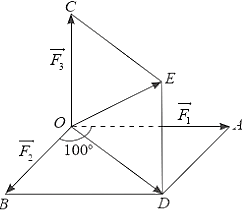
Gọi \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) là ba lực tác động vào vật tại điểm \(O\) lần lượt có độ lớn \(25N,12N,4N\).
Vẽ \(\overrightarrow {OA} = \overrightarrow {{F_1}} ,\overrightarrow {OB} = \overrightarrow {{F_2}} ,\overrightarrow {OC} = \overrightarrow {{F_3}} \).
Dựng hình bình hành \(OADB\) và hình bình hành \(ODEC\).
Hợp lực tác động vào vật là:
\(\overrightarrow F = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OD} + \overrightarrow {OC} = \overrightarrow {OE} .\)
Áp dụng định lí côsin trong tam giác \(OBD\), ta có:
\(O{D^2} = B{D^2} + O{B^2} - 2.BD.OB.\cos \widehat {OBD} = O{A^2} + O{B^2} + 2.OA.OB.\cos 100^\circ \)
Vì \(OC \bot \left( {OADB} \right)\) nên \(OC \bot OD\), suy ra \(ODEC\) là hình chữ nhật.
Do đó, tam giác \(DOE\) vuông tại \(D\).
Ta có: \(O{E^2} = O{C^2} + O{D^2} = O{C^2} + O{A^2} + O{B^2} + 2.OA.OB.\cos 100^\circ \).
Suy ra:
\(OE = \sqrt {O{C^2} + O{A^2} + O{B^2} + 2.OA.OB.\cos 100^\circ } \)\( = \sqrt {{4^2} + {{25}^2} + {{12}^2} + 2.25.12.\cos 100^\circ } \)
\(OE \approx 26N\).
Vậy độ lớn của hợp lực \(F = OE \approx 26N\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.