Sử dụng máy tính cầm tay, tính giá trị của biểu thức \[M = \sin 35^\circ 12' + \cot 20^\circ 25'\] rồi làm tròn kết quả đến hàng phần trăm ta được
A. \[M = 0,949.\]
B. \[M = 0,95.\]
C. \[M = 3,26.\]
D. \[M = 3,263.\]
Quảng cáo
Trả lời:
Đáp án đúng là: C
Ta có: \[\cot 20^\circ 25' = \tan \left( {90^\circ - 20^\circ 25'} \right).\]
Đầu tiên, ta đưa máy tính về chế độ “độ”, sau đó ấn liên tiếp các phím
Màn hình hiện lên kết quả là \(3,262959062,\) làm tròn kết quả đến hàng phần trăm ta được: \(3,26.\)
Nghĩa là, \[M = 3,26.\]
Vậy ta chọn phương án C.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: B
Với \(0^\circ < \alpha < 70^\circ \), ta có: \[90^\circ - \left( {70^\circ - \alpha } \right) = \alpha + 20^\circ ;\,\,\,90^\circ - \left( {80^\circ - \alpha } \right) = \alpha + 10^\circ .\]
Do đó:
\[A = \tan \alpha \cdot \tan \left( {\alpha + 10^\circ } \right) \cdot \tan \left( {\alpha + 20^\circ } \right) \cdot \tan \left( {70^\circ - \alpha } \right) \cdot \tan \left( {80^\circ - \alpha } \right) \cdot \tan \left( {90^\circ - \alpha } \right)\]
\[\,\,\,\,\, = \tan \alpha \cdot \tan \left( {\alpha + 10^\circ } \right) \cdot \tan \left( {\alpha + 20^\circ } \right) \cdot \cot \left( {\alpha + 20^\circ } \right) \cdot \cot \left( {\alpha + 10^\circ } \right) \cdot \cot \alpha \]
\[\,\,\,\,\, = \left( {\tan \alpha \cdot \cot \alpha } \right) \cdot \left[ {\tan \left( {\alpha + 10^\circ } \right) \cdot \cot \left( {\alpha + 10^\circ } \right)} \right] \cdot \left[ {\tan \left( {\alpha + 20^\circ } \right) \cdot \cot \left( {\alpha + 20^\circ } \right)} \right]\]
\[\,\,\,\,\, = 1 \cdot 1 \cdot 1 = 1.\]
</>
Câu 2
A. \[A\] m.
B. \[5\] m.
C. \[6\] m.
D. \[7\] m.
Lời giải
Đáp án đúng là: B
Ta mô hình hóa bài toán như hình vẽ bên.
Khoảng cách từ gốc cây đến điểm bị gãy là \[AB.\]
Khoảng cách từ điểm thân tre bị gãy đến ngọn cây là \[BC.\]
Khoảng cách từ ngọn cây chạm đất đến gốc là \[AC.\]
Đặt độ dài \(BC = x{\rm{\;(m)}}\,\,\left( {0 < x < 9} \right)\).
Suy ra: \(AB = 9 - x.\)
Xét \(\Delta ABC\) vuông tại \(A\) ta có: \(AB = BC \cdot \cos B\)
Suy ra \(9 - x = x \cdot \cos 32^\circ \)
\(9 - x \approx 0,85x\)
\(1,85x \approx 9\)
\[x \approx 4,9{\rm{\;(m)}} \approx {\rm{5\;m}}{\rm{.}}\]
Do đó điểm gãy cách gốc khoảng \(5\) m.
Vậy ta chọn phương án B
</>
Câu 3
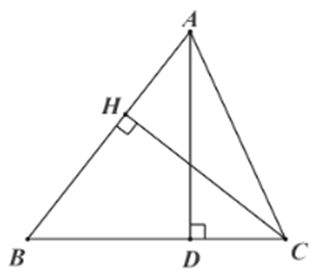
B. \[HC = BC.\cos B.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
D. \[c = a\tan B.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[\sin \alpha = \frac{{EF}}{{DF}}.\]
B. \[\sin \alpha = \frac{{DE}}{{DF}}.\]
C. \[\sin \alpha = \frac{{DE}}{{EF}}.\]
D. \[\sin \alpha = \frac{{EF}}{{DE}}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
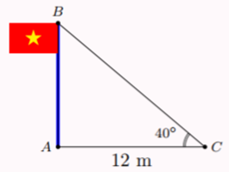
A. \[10,069\] m.
B. \[10,07\] m.
C. \[10,06\] m.
D. \[10,7\] m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Một cây tre cao 9 m bị gió bão làm gãy ngang thân, tạo thành một góc \(32^\circ \).Hỏi điểm gãy \[A\] cách gốc \[B\] khoảng bao nhiêu mét? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid0-1728659459.png)