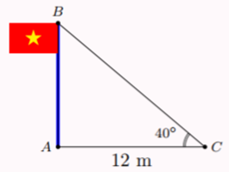
Một cây tre cao 9 m bị gió bão làm gãy ngang thân, tạo thành một góc \(32^\circ \).

Hỏi điểm gãy \[A\] cách gốc \[B\] khoảng bao nhiêu mét?

Đáp án đúng là: B

Với \(0^\circ < \alpha < 70^\circ \), ta có: \[90^\circ - \left( {70^\circ - \alpha } \right) = \alpha + 20^\circ ;\,\,\,90^\circ - \left( {80^\circ - \alpha } \right) = \alpha + 10^\circ .\]

Do đó:

\[A = \tan \alpha \cdot \tan \left( {\alpha + 10^\circ } \right) \cdot \tan \left( {\alpha + 20^\circ } \right) \cdot \tan \left( {70^\circ - \alpha } \right) \cdot \tan \left( {80^\circ - \alpha } \right) \cdot \tan \left( {90^\circ - \alpha } \right)\]

\[\,\,\,\,\, = \tan \alpha \cdot \tan \left( {\alpha + 10^\circ } \right) \cdot \tan \left( {\alpha + 20^\circ } \right) \cdot \cot \left( {\alpha + 20^\circ } \right) \cdot \cot \left( {\alpha + 10^\circ } \right) \cdot \cot \alpha \]

\[\,\,\,\,\, = \left( {\tan \alpha \cdot \cot \alpha } \right) \cdot \left[ {\tan \left( {\alpha + 10^\circ } \right) \cdot \cot \left( {\alpha + 10^\circ } \right)} \right] \cdot \left[ {\tan \left( {\alpha + 20^\circ } \right) \cdot \cot \left( {\alpha + 20^\circ } \right)} \right]\]

\[\,\,\,\,\, = 1 \cdot 1 \cdot 1 = 1.\]

</>

Đáp án đúng là: A

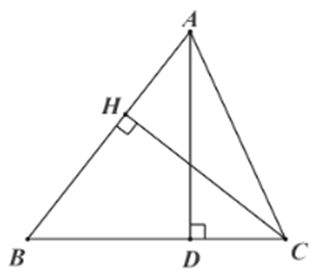
Tam giác \[ABC\] nhọn có \[CH\] là đường cao nên \[CH \bot AB\] tại \[H.\]

Vì tam giác \[BCH\] vuông tại \[H\] nên \[HC = BC.\sin B.\]

Vậy ta chọn phương án A.