Trong không gian Oxyz, cho điểm \(E(2;1;3)\), mặt phẳng \((P):2x + 2y - z - 3 = 0\) và mặt cầu \((S)\): \({(x - 3)^2} + {(y - 2)^2} + {(z - 5)^2} = 36\). Gọi \(\Delta \) là đường thẳng đi qua \(E\), nằm trong mặt phẳng \((P)\) và cắt \((S)\) tại hai điểm A, B có khoảng cách nhỏ nhất.
Đúng
Sai
Điểm E nằm ngoài mặt cầu (S).
Δ có một vectơ chỉ phương là \[\overrightarrow u = ( - 1;1;0)\].
A, B nằm trên đường tròn giao tuyến có tâm là hình chiếu vuông góc của I lên (P).
Trong không gian Oxyz, cho điểm \(E(2;1;3)\), mặt phẳng \((P):2x + 2y - z - 3 = 0\) và mặt cầu \((S)\): \({(x - 3)^2} + {(y - 2)^2} + {(z - 5)^2} = 36\). Gọi \(\Delta \) là đường thẳng đi qua \(E\), nằm trong mặt phẳng \((P)\) và cắt \((S)\) tại hai điểm A, B có khoảng cách nhỏ nhất.
|
Đúng |
Sai |
|
|
Điểm E nằm ngoài mặt cầu (S). |
||
|
Δ có một vectơ chỉ phương là \[\overrightarrow u = ( - 1;1;0)\]. |
||
|
A, B nằm trên đường tròn giao tuyến có tâm là hình chiếu vuông góc của I lên (P). |
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án
|
Đúng |
Sai |
|
|
Điểm E nằm ngoài mặt cầu (S). |
X | |
|
Δ có một vectơ chỉ phương là \[\overrightarrow u = ( - 1;1;0)\]. |
X | |
|
A, B nằm trên đường tròn giao tuyến có tâm là hình chiếu vuông góc của I lên (P). |
X |
Hướng dẫn giải:
![Trong không gian Oxyz, cho điểm \(E(2;1;3)\), mặt phẳng \((P):2x + 2y - z - 3 = 0\) và mặt cầu \((S)\): \({(x - 3)^2} + {(y - 2)^2} + {(z - 5)^2} = 36\). Gọi \(\Delta \) là đường thẳng đi qua \(E\), nằm trong mặt phẳng \((P)\) và cắt \((S)\) tại hai điểm A, B có khoảng cách nhỏ nhất. Đúng Sai Điểm E nằm ngoài mặt cầu (S). Δ có một vectơ chỉ phương là \[\overrightarrow u = ( - 1;1;0)\]. A, B nằm trên đường tròn giao tuyến có tâm là hình chiếu vuông góc của I lên (P). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid11-1729654600.png)
Mặt cầu \((S):{(x - 3)^2} + {(y - 2)^2} + {(z - 5)^2} = 36\), có tâm I(3;2;5) và bán kính R = 6.
Ta có: \(\overrightarrow {EI} = (1;1;2) \Rightarrow EI = |\overrightarrow {EI} | = \sqrt {{1^2} + {1^2} + {2^2}} = \sqrt 6 < 6 = R\). Do đó điểm E nằm trong mặt cầu (S).
Ta lại có: E ∈ (P) và \[\left\{ \begin{array}{l}E \in \Delta \\\Delta \subset \left( P \right)\end{array} \right.\]
Nên giao điểm của (Δ) và (S) nằm trên đường tròn giao tuyến (C) tâm K của mặt phẳng (P) và mặt cầu (S), trong đó K là hình chiếu vuông góc của I lên mặt phẳng (P).
Giả sử Δ ∩ (S) = {A;B}. Độ dài AB nhỏ nhất khi và chỉ khi d(K,Δ) lớn nhất.
Gọi F là hình chiếu của K trên (Δ) khi đó d(K;Δ) = KF ≤ KE.
Dấu bằng xảy ra khi và chỉ khi F ≡ E.
Ta có \(\left\{ \begin{array}{l}IK \bot \left( P \right)\\KE \bot \Delta \end{array} \right. \Rightarrow \left\{ \begin{array}{l}IK \bot \Delta \\KE \bot \Delta \end{array} \right. \Rightarrow IE \bot \Delta \).
Ta có: \(\left[ {{{\vec n}_{(P)}},\overrightarrow {EI} } \right] = (5; - 5;0)\), cùng phương với \[\overrightarrow u = (1; - 1;0).\]
Vì \(\left\{ \begin{array}{l}\Delta \subset \left( P \right)\\\Delta \bot IE\end{array} \right.\) nên Δ có một vectơ chỉ phương là \[\overrightarrow u = (1; - 1;0).\]
Suy ra phương trình đường thẳng Δ:\(\left\{ \begin{array}{l}x = 2 + t\\y = 1 - t\\z = 3\end{array} \right.\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 741,2 m.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
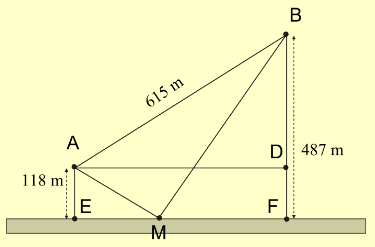
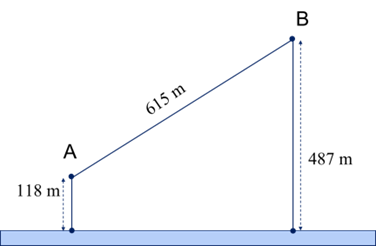
Giả sử người đó đi từ A đến M để lấy nước và đi từ M về B. Dễ dàng tính được BD = 369, EF = 492. Ta đặt EM = x, khi đó:
\(MF = 492 - x,AM = \sqrt {{x^2} + {{118}^2}} ,BM = \sqrt {{{(492 - x)}^2} + {{487}^2}} .\)
Như vậy ta có hàm số f(x) được xác định bằng tổng quãng đường AM và MB :
\(f(x) = \sqrt {{x^2} + {{118}^2}} + \sqrt {{{(492 - x)}^2} + {{487}^2}} \) với \(x \in [0;492]\)
Ta cần tìm giá trị nhỏ nhất của f(x) để có quãng đường ngắn nhất và từ đó xác định được vị trí điểm M.
\(f'(x) = \frac{x}{{\sqrt {{x^2} + {{118}^2}} }} - \frac{{492 - x}}{{\sqrt {{{(492 - x)}^2} + {{487}^2}} }}\)
\(f'(x) = 0 \Leftrightarrow \frac{x}{{\sqrt {{x^2} + {{118}^2}} }} - \frac{{492 - x}}{{\sqrt {{{(492 - x)}^2} + {{487}^2}} }} = 0\)
\( \Leftrightarrow \frac{x}{{\sqrt {{x^2} + {{118}^2}} }} = \frac{{492 - x}}{{\sqrt {{{(492 - x)}^2} + {{487}^2}} }}\)
\( \Leftrightarrow x\sqrt {{{(492 - x)}^2} + {{487}^2}} = (492 - x)\sqrt {{x^2} + {{118}^2}} \)
\( \Leftrightarrow \left\{ \begin{array}{l}{x^2}\left[ {{{(492 - x)}^2} + {{487}^2}} \right] = {\left( {492 - x} \right)^2}\left( {{x^2} + {{118}^2}} \right)\\0 \le x \le 492\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{(487x)^2} = {(58056 - 118x)^2}\\0 \le x \le 492\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x = \frac{{58056}}{{605}}{\rm{ hay }}x = - \frac{{58056}}{{369}}\\0 \le x \le 492\end{array} \right.\)
\( \Leftrightarrow x = \frac{{58056}}{{605}}\)
Hàm số \(f(x)\) liên tục trên đoạn [0; 492]. So sánh các giá trị của \(f(0),f\left( {\frac{{58056}}{{605}}} \right),f(492)\) ta có giá trị nhỏ nhất là \(f\left( {\frac{{58056}}{{605}}} \right) \approx 779,8\;{\rm{m}}\).
Chọn B
Câu 2
A. \({\rm{C}}{{\rm{H}}_3}{\rm{COOH}} + {\rm{CH}} \equiv {\rm{CH}} \to {\rm{C}}{{\rm{H}}_3}{\rm{COOCH}} = {\rm{C}}{{\rm{H}}_2}\).
B. \({\rm{C}}{{\rm{H}}_2} = {\rm{CHCOOH}} + {\rm{C}}{{\rm{H}}_3}{\rm{OH}} \to {\rm{C}}{{\rm{H}}_2} = \) \({\rm{CHCOOC}}{{\rm{H}}_3} + {{\rm{H}}_2}{\rm{O}}\).
C. \({\rm{C}}{{\rm{H}}_3}{\rm{COOH}} + {\rm{C}}{{\rm{H}}_2} = {\rm{CHOH}} \to {\rm{C}}{{\rm{H}}_3}{\rm{COOCH}} = \) \({\rm{C}}{{\rm{H}}_2} + {{\rm{H}}_2}{\rm{O}}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải:
Không thể điều chế trực tiếp vinyl axetat từ axit axetic và ancol vinylic vì ancol này không bền, do đó phải thực hiện phản ứng giữa axit axetic và axetilen.
Chọn A
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập