Tìm tất cả các giá trị thực của tham số \(m\) để bất phương trình sau có nghiệm: \(m{\log _{3 - \sqrt {4 - x} }}3 \ge x\sqrt x + \sqrt {x + 12} \).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải:
ĐK: \(\left\{ \begin{array}{l}3 - \sqrt {4 - x} > 0\\3 - \sqrt {4 - x} \ne 1\\x \ge 0\\x + 12 \ge 0\\4 - x \ge 0\end{array} \right. \Leftrightarrow 0 \le x \le 4\).
Nhận xét: \(3 - \sqrt {4 - x} > 3 - \sqrt {4 - 0} = 1 \Rightarrow {\log _{3 - \sqrt {4 - x} }}3 > {\log _{3 - \sqrt {4 - x} }}1 = 0\).
\(m{\log _{3 - \sqrt {4 - x} }}3 \ge x\sqrt x + \sqrt {x + 12} \Leftrightarrow m \ge \frac{{x\sqrt x + \sqrt {x + 12} }}{{{{\log }_{3 - \sqrt {4 - x} }}3}} \Leftrightarrow m \ge \left( {x\sqrt x + \sqrt {x + 12} } \right).{\log _3}\left( {3 - \sqrt {4 - x} } \right)\)
Đặt \(f(x) = \left( {x\sqrt x + \sqrt {x + 12} } \right).{\log _3}\left( {3 - \sqrt {4 - x} } \right)\)
\({f^\prime }(x) = \left( {\frac{3}{2}\sqrt x + \frac{2}{{2\sqrt {x + 12} }}} \right){\log _3}\left( {3 - \sqrt {4 - x} } \right) + \left( {x\sqrt x + \sqrt {x + 12} } \right).\frac{1}{{\left( {3 - \sqrt {4 - x} } \right)\ln 3.2\sqrt {4 - x} }}\)
Vì \(f'(x) > 0,\forall x \in (0;4) \Rightarrow f(x)\) tăng trên (0;4) ⇒ tập giá trị của f(x) là (0;12).
Vậy bất phương trình có nghiệm khi và chỉ khi m > 0.
Chọn C
Đang tải chế độ Học...
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
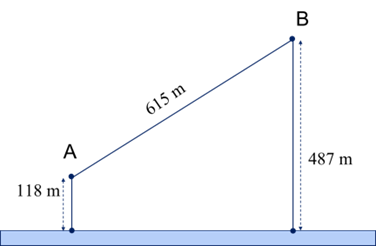
A. 741,2 m.
Lời giải
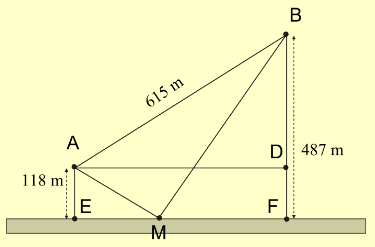
Giả sử người đó đi từ A đến M để lấy nước và đi từ M về B. Dễ dàng tính được BD = 369, EF = 492. Ta đặt EM = x, khi đó:
\(MF = 492 - x,AM = \sqrt {{x^2} + {{118}^2}} ,BM = \sqrt {{{(492 - x)}^2} + {{487}^2}} .\)
Như vậy ta có hàm số f(x) được xác định bằng tổng quãng đường AM và MB :
\(f(x) = \sqrt {{x^2} + {{118}^2}} + \sqrt {{{(492 - x)}^2} + {{487}^2}} \) với \(x \in [0;492]\)
Ta cần tìm giá trị nhỏ nhất của f(x) để có quãng đường ngắn nhất và từ đó xác định được vị trí điểm M.
\(f'(x) = \frac{x}{{\sqrt {{x^2} + {{118}^2}} }} - \frac{{492 - x}}{{\sqrt {{{(492 - x)}^2} + {{487}^2}} }}\)
\(f'(x) = 0 \Leftrightarrow \frac{x}{{\sqrt {{x^2} + {{118}^2}} }} - \frac{{492 - x}}{{\sqrt {{{(492 - x)}^2} + {{487}^2}} }} = 0\)
\( \Leftrightarrow \frac{x}{{\sqrt {{x^2} + {{118}^2}} }} = \frac{{492 - x}}{{\sqrt {{{(492 - x)}^2} + {{487}^2}} }}\)
\( \Leftrightarrow x\sqrt {{{(492 - x)}^2} + {{487}^2}} = (492 - x)\sqrt {{x^2} + {{118}^2}} \)
\( \Leftrightarrow \left\{ \begin{array}{l}{x^2}\left[ {{{(492 - x)}^2} + {{487}^2}} \right] = {\left( {492 - x} \right)^2}\left( {{x^2} + {{118}^2}} \right)\\0 \le x \le 492\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{(487x)^2} = {(58056 - 118x)^2}\\0 \le x \le 492\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x = \frac{{58056}}{{605}}{\rm{ hay }}x = - \frac{{58056}}{{369}}\\0 \le x \le 492\end{array} \right.\)
\( \Leftrightarrow x = \frac{{58056}}{{605}}\)
Hàm số \(f(x)\) liên tục trên đoạn [0; 492]. So sánh các giá trị của \(f(0),f\left( {\frac{{58056}}{{605}}} \right),f(492)\) ta có giá trị nhỏ nhất là \(f\left( {\frac{{58056}}{{605}}} \right) \approx 779,8\;{\rm{m}}\).
Chọn B
Câu 2
A. \({\rm{C}}{{\rm{H}}_3}{\rm{COOH}} + {\rm{CH}} \equiv {\rm{CH}} \to {\rm{C}}{{\rm{H}}_3}{\rm{COOCH}} = {\rm{C}}{{\rm{H}}_2}\).
B. \({\rm{C}}{{\rm{H}}_2} = {\rm{CHCOOH}} + {\rm{C}}{{\rm{H}}_3}{\rm{OH}} \to {\rm{C}}{{\rm{H}}_2} = \) \({\rm{CHCOOC}}{{\rm{H}}_3} + {{\rm{H}}_2}{\rm{O}}\).
C. \({\rm{C}}{{\rm{H}}_3}{\rm{COOH}} + {\rm{C}}{{\rm{H}}_2} = {\rm{CHOH}} \to {\rm{C}}{{\rm{H}}_3}{\rm{COOCH}} = \) \({\rm{C}}{{\rm{H}}_2} + {{\rm{H}}_2}{\rm{O}}\).
Lời giải
Hướng dẫn giải:
Không thể điều chế trực tiếp vinyl axetat từ axit axetic và ancol vinylic vì ancol này không bền, do đó phải thực hiện phản ứng giữa axit axetic và axetilen.
Chọn A
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập