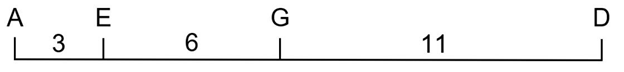Kéo thả số thích hợp vào ô trống
Một vật chuyển động theo quy luật \(s = - \frac{1}{2}{t^3} + 3{t^2} + 20\) với t (giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và s (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó.
a) Quãng đường vật đi được tính từ lúc xuất phát đến lúc vật đạt vận tốc lớn nhất bằng ... .
b) Quãng đường vật đi được từ lúc xuất phát đến lúc vật dừng hẳn bằng ....
Một vật chuyển động theo quy luật \(s = - \frac{1}{2}{t^3} + 3{t^2} + 20\) với t (giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và s (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó.
a) Quãng đường vật đi được tính từ lúc xuất phát đến lúc vật đạt vận tốc lớn nhất bằng ... .
b) Quãng đường vật đi được từ lúc xuất phát đến lúc vật dừng hẳn bằng ....Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Quãng đường vật đi được tính từ lúc xuất phát đến lúc vật đạt vận tốc lớn nhất bằng 28m .
Ta có \(v(t) = s' = - \frac{3}{2}{t^2} + 6t\). Ta đi tìm \(\mathop {\max }\limits_{\left( {0; + \infty } \right)} v(t)\).
\(v'(t) = - 3t + 6 \Rightarrow v'(t) = 0 \Leftrightarrow t = 2\)
Bảng biến thiên:
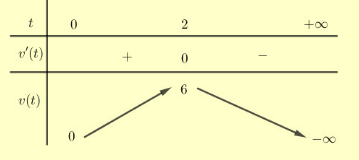
Từ bảng biến thiên ta có:
\( + )\mathop {\max }\limits_{(0; + \infty )} v(t) = v(2) = 6.\)
Vậy quãng đường vật đi được đến lúc đạt vận tốc lớn nhất là: \(s = - \frac{1}{2}{.2^3} + {3.2^2} + 20 = 28\;{\rm{m}}\).
+ ) Vật dừng lại ở thời điểm \(t\) thỏa mãn \(t > 0\) và \(v(t) = 0 \Leftrightarrow - \frac{3}{2}{t^2} + 6t = 0 \Leftrightarrow t = 4\).
Quãng đường vật di chuyển được là: \(s(4) = 36\;{\rm{m}}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
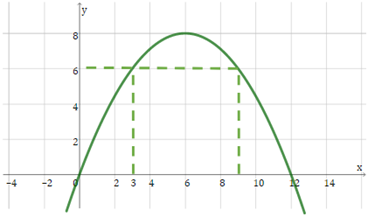
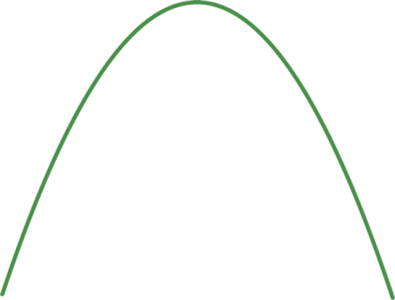
Chọn hệ trục tọa độ như hình vẽ. Parabol có phương trình dạng \(y = a{x^2} + bx\).
Vì chiếc cổng hình parabol có chiều rộng 12 m và chiều cao, theo hình vẽ ta có parabol đi qua các điểm (12;0) và (6;8), suy ra: \(\left\{ {\begin{array}{*{20}{l}}{144a + 12b = 0}\\{36a + 6b = 8}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = - \frac{2}{9}}\\{b = \frac{8}{3}}\end{array}.} \right.} \right.\)
Suy ra parabol có phương trình \(y = - \frac{2}{9}{x^2} + \frac{8}{3}\).
Do chiếc xe tải có chiều ngang 6 m đi vào vị trí chính giữa cổng nên xe sẽ chạm tường tại điểm A(3;6) khi đó chiều cao của xe là 6 m.
Vậy điều kiện để xe tải có thể đi vào cổng mà không chạm tường là 0 < h < 6.
Câu 2
A. Vì không thể hàn hai thanh ray với nhau.
B. Vì để tiết kiệm vật liệu.
C. Vì để vậy sẽ lắp các thanh ray dễ dàng hơn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải:
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. A và G.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập