Câu hỏi:
25/10/2024 1,064
Định luật làm mát của Newton phát biểu rằng tốc độ làm mát của một vật tỉ lệ thuận với chênh lệch nhiệt độ giữa vật đó và môi trường xung quanh, với điều kiện là chênh lệch này không quá lớn. Giả sử \(T\left( t \right)\) là nhiệt độ của vật thể (đơn vị: độ C) tại thời điểm \(t\) (đơn vị: phút) và \({T_s}\) là nhiệt độ của môi trường xung quanh, chênh lệch giữa nhiệt độ của vật thể và môi trường xung quanh là
\(y\left( t \right) = T\left( t \right) - {T_s}\) thì \(\frac{{y'\left( t \right)}}{{y\left( t \right)}} = k\) với \(k\) là hằng số.
Một cốc nước đang ở nhiệt độ phòng là \({22^ \circ }{\rm{C}}\) được đưa vào ngăn mát tủ lạnh có nhiệt độ là \({5^ \circ }{\rm{C}}\). Sau 30 phút, nhiệt độ của cốc nước được đo lại là \({16^ \circ }C\). Giả sử \(T\left( t \right)\) là nhiệt độ của cốc nước, \(y\left( t \right)\) là nhiệt độ chênh lệch giữa cốc nước và nhiệt độ ngăn mát tủ lạnh sau khoảng thời gian \(t\).
Mỗi phát biểu sau đây là đúng hay sai?
Phát biểu
Đúng
Sai
Nhiệt độ của chênh lệch giữa cốc nước và nhiệt độ ngăn mát tủ lạnh sau khoảng thời gian \(t\) là hàm số có dạng \(y\left( t \right) = y\left( 0 \right){e^{kt}}\)
Kết quả làm tròn đến chữ số thập phân thứ tư của \(k\) là \( - 0,0145\).
Sau 60 phút trong tủ lạnh, nhiệt độ của cốc nước khoảng \({10^ \circ }C\) (Kết quả làm
tròn đến chữ số hàng đơn vị).
Định luật làm mát của Newton phát biểu rằng tốc độ làm mát của một vật tỉ lệ thuận với chênh lệch nhiệt độ giữa vật đó và môi trường xung quanh, với điều kiện là chênh lệch này không quá lớn. Giả sử \(T\left( t \right)\) là nhiệt độ của vật thể (đơn vị: độ C) tại thời điểm \(t\) (đơn vị: phút) và \({T_s}\) là nhiệt độ của môi trường xung quanh, chênh lệch giữa nhiệt độ của vật thể và môi trường xung quanh là
\(y\left( t \right) = T\left( t \right) - {T_s}\) thì \(\frac{{y'\left( t \right)}}{{y\left( t \right)}} = k\) với \(k\) là hằng số.
Một cốc nước đang ở nhiệt độ phòng là \({22^ \circ }{\rm{C}}\) được đưa vào ngăn mát tủ lạnh có nhiệt độ là \({5^ \circ }{\rm{C}}\). Sau 30 phút, nhiệt độ của cốc nước được đo lại là \({16^ \circ }C\). Giả sử \(T\left( t \right)\) là nhiệt độ của cốc nước, \(y\left( t \right)\) là nhiệt độ chênh lệch giữa cốc nước và nhiệt độ ngăn mát tủ lạnh sau khoảng thời gian \(t\).
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Nhiệt độ của chênh lệch giữa cốc nước và nhiệt độ ngăn mát tủ lạnh sau khoảng thời gian \(t\) là hàm số có dạng \(y\left( t \right) = y\left( 0 \right){e^{kt}}\) |
||
|
Kết quả làm tròn đến chữ số thập phân thứ tư của \(k\) là \( - 0,0145\). |
||
|
Sau 60 phút trong tủ lạnh, nhiệt độ của cốc nước khoảng \({10^ \circ }C\) (Kết quả làm tròn đến chữ số hàng đơn vị). |
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Nhiệt độ của chênh lệch giữa cốc nước và nhiệt độ ngăn mát tủ lạnh sau khoảng thời gian \(t\) là hàm số có dạng \(y\left( t \right) = y\left( 0 \right){e^{kt}}\) |
X | |
|
Kết quả làm tròn đến chữ số thập phân thứ tư của \(k\) là \( - 0,0145\). |
X | |
|
Sau 60 phút trong tủ lạnh, nhiệt độ của cốc nước khoảng \({10^ \circ }C\) (Kết quả làm tròn đến chữ số hàng đơn vị). |
X |
Giải thích
|
Lí do lựa chọn phương án
|
1) |
Đúng vì: Do \(\frac{{y'\left( t \right)}}{{y\left( t \right)}} = k\) với \(k\) là hằng số. Lấy tích phân với cận từ 0 đến \(t\) hai vế. Ta được \(\int\limits_0^t {\frac{{y'\left( t \right)}}{{y\left( t \right)}}dt} = \int\limits_0^t {kdt} \) Kéo theo \({\rm{ln}}\frac{{y\left( t \right)}}{{y\left( 0 \right)}} = kt\), hay \(y\left( t \right) = y\left( 0 \right).{e^{kt}}\). |
|
2) |
Đúng vì: Tính được \(y\left( 0 \right) = T\left( 0 \right) - {T_s} = 22 - 5 = 17\). Ta có \(T\left( t \right) = {T_s} + y\left( t \right) = 5 + 17{e^{kt}}\). Thay \(t = 30\) ta được \(T\left( {30} \right) = 5 + 17{e^{30k}}\). Mà \(T\left( {30} \right) = 16\) nên \(k = {\rm{ln}}\left( {\frac{{11}}{{17}}} \right):30 \approx - 0,0145\). |
|
|
3) |
Sai vì: Tính \(T\left( {60} \right) \approx 12\) (Kết quả làm tròn đến chữ số hàng đơn vị). |
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
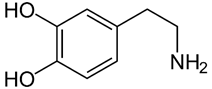
Theo đoạn văn: “Dopamine có công thức phân tử là C8H11NO2 (3,4-dihydroxyphenethylamine)” nên dopamine còn có tên gọi là 4-(2-aminoethyl)benzene-1,2-diol và công thức cấu tạo:
Chọn B
Lời giải
Theo bài đọc: “Dưới tác dụng của một số enzyme, tinh bột trong nông sản sẽ bị thủy phân tạo thành đường glucose.”
Chọn C
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 1)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 24)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 2)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 18)
-
ĐGTD ĐH Bách khoa - Đọc hiểu chủ đề môi trường - Đề 1
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 6)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 4)
-
ĐGTD ĐH Bách khoa - Tư duy Toán học - Xác suất của biến cố và các quy tắc tính xác suất
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận