Câu hỏi:
14/11/2024 21Cho tam giác đều \[ABC\] có tâm \[O\] và các đường cao \[AA',BB',CC'\]. Phép quay thuận chiều tâm \[O\] góc \(240^\circ \) biến đường cao \[AA'\] thành
Đáp án chính xác
Câu hỏi trong đề:
15 câu trắc nghiệm Toán 9 Cánh diều Bài 2. Phép quay có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: B
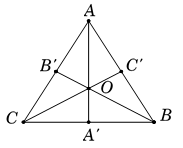
Do tam giác \[ABC\] đều nên \(\widehat {A'OB'} = \widehat {B'OC'} = \widehat {C'OA'} = 120^\circ \).
Khi đó xét phép quay tâm \[O\] góc quay \(240^\circ \):
Biến \[A\] thành \[B\] .
Biến \[A'\] thành \[B'\].
Vậy phép quay thuận chiều tâm \[O\] góc \(240^\circ \) biến đường cao \[AA'\] thành \[BB'\].
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác \[ABC\] vuông tại \[B\] và góc tại \[A\] bằng \(60^\circ \). Về phía ngoài tam giác vẽ tam giác đều \[ACD\]. Phép quay tâm \[A\] góc \(60^\circ \) biến \[BC\] thành
Xem đáp án »
14/11/2024
23
Câu 2:
III. Vận dụng
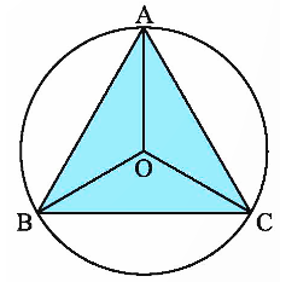
Cho tam giác \[ABC\] đều nội tiếp đường tròn \[\left( O \right).\] Các phép quay giữ nguyên tam giác \[ABC\] là
Xem đáp án »
14/11/2024
22
Câu 3:
Cho tam giác đều \[ABC\]. Góc quay của phép quay thuận chiều tâm A biến B thành C là
Xem đáp án »
14/11/2024
16
Câu 4:
Khi quay thuận chiều \(\alpha ^\circ \) tâm \[O\] điểm \[A\] thành điểm \[B\] thì điểm \[A\] tạo thành cung \[AB\] có số đo bằng
Xem đáp án »
14/11/2024
15
Câu 5:
Cho hình thoi \[ABCD\] có góc \(\widehat {ABC} = 60^\circ \). Phép quay thuận chiều tâm \[A\] một góc \(60^\circ \) biến cạnh \[CD\] thành
Xem đáp án »
14/11/2024
14
Câu 6:
Cho hình ngũ giác đều \[ABCDE\] tâm \[O\]. Phép quay thuận chiều tâm \[O\] biến điểm \[A\] thành điểm \[E\] thì điểm \[C\] biến thành điểm
Xem đáp án »
14/11/2024
14
về câu hỏi!