Cho 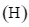 là đa giác đều
là đa giác đều  đỉnh nội tiếp đường tròn tâm
đỉnh nội tiếp đường tròn tâm 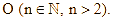 Gọi
Gọi 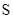 là tập hợp các tam giác có 3 đỉnh là các đỉnh của đa giác
là tập hợp các tam giác có 3 đỉnh là các đỉnh của đa giác 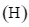 . Chọn ngẫu nhiên một tam giác thuộc tập
. Chọn ngẫu nhiên một tam giác thuộc tập 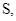 biết rằng xác suất chọn một tam giác vuông trong tập
biết rằng xác suất chọn một tam giác vuông trong tập 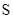 là
là 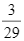 . Tìm
. Tìm  (nhập đáp án vào ô trống).
(nhập đáp án vào ô trống).

Cho ![]() là đa giác đều
là đa giác đều ![]() đỉnh nội tiếp đường tròn tâm
đỉnh nội tiếp đường tròn tâm 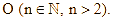 Gọi
Gọi ![]() là tập hợp các tam giác có 3 đỉnh là các đỉnh của đa giác
là tập hợp các tam giác có 3 đỉnh là các đỉnh của đa giác ![]() . Chọn ngẫu nhiên một tam giác thuộc tập
. Chọn ngẫu nhiên một tam giác thuộc tập ![]() biết rằng xác suất chọn một tam giác vuông trong tập
biết rằng xác suất chọn một tam giác vuông trong tập ![]() là
là ![]() . Tìm
. Tìm ![]() (nhập đáp án vào ô trống).
(nhập đáp án vào ô trống).
![]()
Quảng cáo
Trả lời:
Số phần tử của không gian mẫu ![]()
Tam giác vuông được chọn là tam giác chứa cạnh là đường kính của đường tròn tâm ![]()
Đa giác đều 2n đỉnh chứa n đường chéo là đường kính của đường tròn tâm ![]() mỗi đường kính tạo nên
mỗi đường kính tạo nên ![]() tam giác vuông.
tam giác vuông.
Do đó số tam giác vuông trong tập ![]() là:
là: ![]()
Xác suất chọn một tam giác vuông trong tập ![]() là:
là:
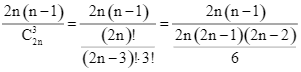
![]() .
.
Đáp án cần nhập là: 15.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. Giọng điệu, ngôn ngữ biến đổi linh hoạt.
C. Lời văn giàu tính biểu cảm.
D. Ngôn ngữ hùng hồn nhưng gần gũi.
Lời giải
Câu 2
Lời giải
Đáp án đúng là A
Gọi số hạt nhân ![]() và số hạt nhân
và số hạt nhân ![]() tại thời điểm ban đầu là
tại thời điểm ban đầu là ![]() và
và ![]()
Sau thời gian t, số hạt nhân ![]() còn lại là:
còn lại là: ![]() .
.
Số hạt nhân ![]() mới được tạo thành bằng số hạt nhân
mới được tạo thành bằng số hạt nhân ![]() đã mất đi:
đã mất đi:
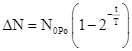
Tại thời điểm ![]() , tỉ số giữa số hạt nhân
, tỉ số giữa số hạt nhân ![]() và số hạt nhân
và số hạt nhân ![]() là:
là:

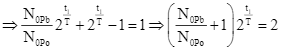 (1)
(1)
Tại thời điểm t2, tỉ số giữa số hạt nhân ![]() và số hạt nhân
và số hạt nhân ![]() là:
là:
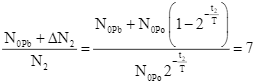
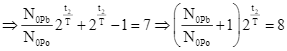 (2)
(2)
Chia (2) cho (1) theo từng vế: 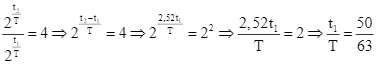
Thay vào (1) ta tìm được tỉ số: ![]()
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Đại hội quốc dân họp ở Tân Trào (8/1945).
B. Hội nghị đại biểu toàn quốc của Đảng (8/1945).
C. Tiến hành Tổng tuyển cử bầu Quốc hội (1/1946).
D. Hồ Chí Minh đọc Tuyên ngôn độc lập (2/9/1945).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.