Câu hỏi:
11/12/2024 973
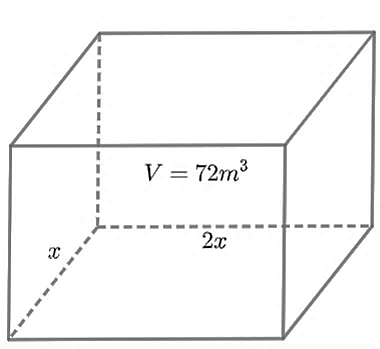
Bác Sơn muốn xây một bể chứa nước có dạng hình hộp chữ nhật không nắp có thể tích bằng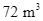 
. Đáy bể có dạng hình chữ nhật với chiều rộng là 
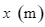, chiều dài gấp đôi chiều rộng. Bác Sơn muốn phần diện tích cần xây (bao gồm diện tích xung quanh và diện tích đáy bể) là nhỏ nhất để tiết kiệm chi phí thì 
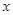phải bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
Bác Sơn muốn xây một bể chứa nước có dạng hình hộp chữ nhật không nắp có thể tích bằng . Đáy bể có dạng hình chữ nhật với chiều rộng là , chiều dài gấp đôi chiều rộng. Bác Sơn muốn phần diện tích cần xây (bao gồm diện tích xung quanh và diện tích đáy bể) là nhỏ nhất để tiết kiệm chi phí thì phải bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 9 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chiều dài của đáy bể là 
Diện tích đáy của bể là 
Chiều cao của bể là: 
.
Diện tích xung quanh của bể là: 
Diện tích cần xây bằng tổng diện tích xung quanh và diện tích đáy của bể, và bằng:
Do 
là chiều rộng của bể nên 
, áp dụng bất đẳng thức Cauchy, ta có:
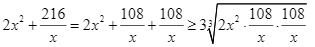
Suy ra 
Dấu “=” xảy ra khi 
hay 
, tức là 
Vậy muốn diện tích cần xây là tiết kiệm chi phí nhất thì 
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: C
Bán kính của đường tròn lớn là: 
Bán kính của đường tròn nhỏ là: 
Diện tích bề mặt trên chiếc đèn chính là diện tích hình vành khuyên được giới hạn bởi hai đường tròn có bán kính lần lượt là 
và bằng:
Lời giải
Vì 
và 
là tiếp tuyến của đường tròn tâm 
nên 
, 
, do đó 
. Gọi 
là trung điểm của 
.
Xét 
vuông tại 
có 
là đường trung tuyến ứng với cạnh huyền nên 
(1).
Xét 
vuông tại 
có 
là đường trung tuyến ứng với cạnh huyền nên 
(2).
Từ (1) và (2) suy ra 
.
Vậy các điểm 
cùng thuộc một đường tròn tâm đường kính .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Chuyên đề 8: Hình học (có đáp án)
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận