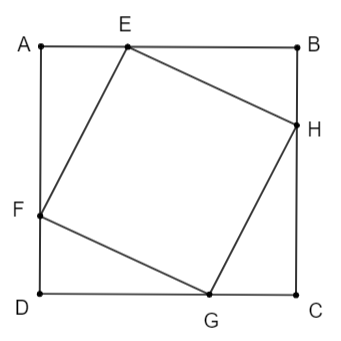
Bác An có mảnh vườn hình vuông 
có cạnh bằng 
. Ở bốn góc vườn, bác An muốn trồng hoa vào các phần đất hình tam giác vuông bằng nhau (hình vẽ). Hãy tính khoảng cách từ góc vườn 
đến vị trí 
sao cho tứ giác 
có chu vi nhỏ nhất.
có cạnh bằng 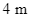. Ở bốn góc vườn, bác An muốn trồng hoa vào các phần đất hình tam giác vuông bằng nhau (hình vẽ). Hãy tính khoảng cách từ góc vườn 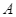đến vị trí 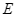sao cho tứ giác 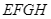có chu vi nhỏ nhất.
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 9 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi độ dài của đoạn AE = x (0 < x < 4) (m), suy ra độ dài đoạn 
Theo đề, các phần đất hình tam giác bằng nhau, nên ta có:
và 
.
Áp dụng định lí Pythagore vào tam giác 
vuông tại 
, có:
Suy ra 
Do các phần hình tam giác bằng nhau nên 
.
Suy ra, chu vi 
là: 
.
Để chu vi của tứ giác nhỏ nhất thì 
nhỏ nhất.
Với mọi 
ta có:
.
Do đó, chu vi của tứ giác nhỏ nhất bằng 
khi 
hay 
Vậy khoảng cách từ đến 
bằng 
thì tứ giác có chu vi nhỏ nhất.
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi 
lần lượt là khối lượng táo, xoài mà bác Nam mua (
đơn vị: kg).
Theo bài, bác Nam mua một thùng trái cây nặng 
kg gồm hai loại là táo và xoài nên ta có phương trình: 
(1)
Số tiền bác Nam dùng để mua táo là: 
(nghìn đồng).
Số tiền bác Nam dùng để mua xoài là: 
(nghìn đồng).
Theo bài, giá tiền của thùng trái cây là 
đồng (hay 
nghìn đồng) nên ta có phương trình: nên 
(2)
Từ (1) và (2) ta có hệ phương trình 
Từ phương trình (1), ta có: 
, thế vào phương trình (2), ta được:
(thỏa mãn).
Thay vào phương trình , ta được: 
(thỏa mãn).
Vậy bác Nam đã mua 11 kg táo và 7 kg xoài.
Lời giải
⦁ Chứng minh tam giác 
là tam giác cân
Theo câu b, 
suy ra 
.
Xét 
và 
có: 
là góc chung và
Do đó 
(c.g.c), suy ra 
(hai góc tương ứng).
Ta có: 
nên tam giác 
cân ở 
, suy ra 
.
Mà 
suy ra 
nên 
.
Xét 
cân ở (do 
) có 
là đường cao nên cũng là đường trung trực của 
. Suy ra 
nên 
cân ở 
.
⦁ Xác định vị trí của để chu vi tứ giác 
lớn nhất
Chứng minh tương tự câu c, ta có 
là tiếp tuyến của đường tròn 
tại 
Ta có: 
suy ra 
, do đó tứ giác là hình thang.
Lại có 
nên hình thang là hình thang vuông.
Ta có chu vi là 
(do 
.
Lại có 
và 
Do đó 
, suy ra 
Hay 
.
Dấu “=” xảy ra khi và chỉ khi 
. Mà 
(chứng minh ở câu c) nên 
Lại có 
là đường kính của đường tròn 
và điểm nằm trên đường tròn nên lúc này điểm 
trùng điểm 
tức là 
tại tâm . Như vậy, điều này xảy ra khi và chỉ khi nằm chính giữa cung .
Vậy chu vi đạt giá trị lớn nhất là 
khi nằm chính giữa cung .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập