Sử dụng dữ kiện của bài toán dưới đây để trả lời cho Bài 8, 9 , 10.
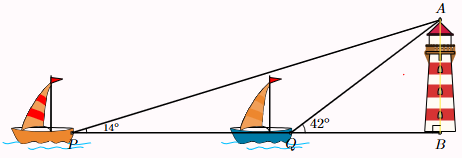
Hai con thuyền P và Q cách nhau 300 m và thẳng hàng với chân B của tháp hải đăng ở trên bờ biển. Từ P và Q, người ta nhìn thấy tháp hải đăng dưới các góc \(\widehat {BPQ} = 14^\circ \) và \(\widehat {BQA} = 42^\circ \). Đặt h = AB là chiều cao của tháp hải đăng.
Sử dụng dữ kiện của bài toán dưới đây để trả lời cho Bài 8, 9 , 10.
Hai con thuyền P và Q cách nhau 300 m và thẳng hàng với chân B của tháp hải đăng ở trên bờ biển. Từ P và Q, người ta nhìn thấy tháp hải đăng dưới các góc \(\widehat {BPQ} = 14^\circ \) và \(\widehat {BQA} = 42^\circ \). Đặt h = AB là chiều cao của tháp hải đăng.
Độ dài BQ theo h là
A. \(\frac{h}{{\tan 42^\circ }}\).
B. \(\frac{h}{{\cot 42^\circ }}\).
C. \(\frac{h}{{\tan 14^\circ }}\).
D. \(\frac{h}{{\cot 14^\circ }}\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: A
Xét tam giác BQA vuông tại B, ta có:
tanQ = \(\frac{{AB}}{{QB}}\) nên BQ = \(\frac{{AB}}{{QB}}\) nên BQ = \(\frac{{AB}}{{\tan 42^\circ }} = \frac{h}{{\tan 42^\circ }}\).
Câu hỏi cùng đoạn
Câu 2:
Độ dài BP theo h là
A. \(\frac{h}{{\tan 42^\circ }}\).
B. \(\frac{h}{{\cot 42^\circ }}\).
C. \(\frac{h}{{\tan 14^\circ }}\).
D. \(\frac{h}{{\cot 14^\circ }}\).
Giải bởi Vietjack
Đáp án đúng là: C
Xét tam giác BPA vuông tại B, ta có:
tanP = \(\frac{{AB}}{{PB}}\) nên \(PB = \frac{{AB}}{{\tan 14^\circ }} = \frac{h}{{\tan 14^\circ }}\).
Câu 3:
Chiều cao cuủa tháp hải đăng (làm tròn đến hàng phần mười) là:
A. 103 m.
B. 103,4 m.
C. 104 m.
D. 104,3 m.
Giải bởi Vietjack
Đáp án đúng là: B
Ta có: BP – BQ = 300.
Suy ra \(\frac{h}{{\tan 42^\circ }} - \frac{h}{{\tan 14^\circ }} = 300\).
Suy ra h = \(\frac{{300}}{{\frac{1}{{\tan 14^\circ }} - \frac{1}{{\tan 42^\circ }}}} \approx 103,4\) (m).
Vậy chiều cao của tháp hải đăng là khoảng 103,4 m.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 326 m.
B. 362 m.
C. 236 m.
D. 263 m.
Lời giải
Đáp án đúng là: A
Xét tam giác ADC vuông tại C, ta có: AC = h.cot\(\widehat {DAC}\) = h.cot60° (m)
Xét tam giác BDC vuông tại C, ta có: BC = h.cot\(\widehat {DBC}\) = h.cot75° (m).
Do AC – BC = AB = 101 nên h.cot60° − h.cot75° = 101
Suy ra h = \(\frac{{101}}{{\cot 60^\circ - \cot 75^\circ }} \approx 326\) (m).
Vậy tháp Eiffel có độ cao khoảng 326 (m).
Câu 2
A. 196 m.
B. 277 m.
C. 169 m.
D. 275 m.
Lời giải
Đáp án đúng là: A
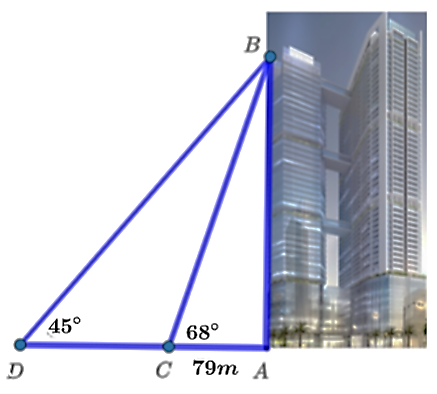
Chiều cao của tòa tháp chính là độ dài của đoạn AB.
Xét tam giác ABC vuông tại A, ta có: AB = AC. \(\tan \widehat {ACB}\) = 79.tan68° ≈ 196 m.
Sử dụng dữ kiện bài toán sau để trả lời Bài 2, 3.
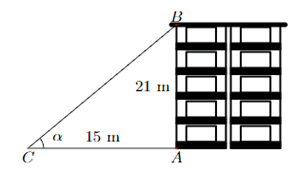
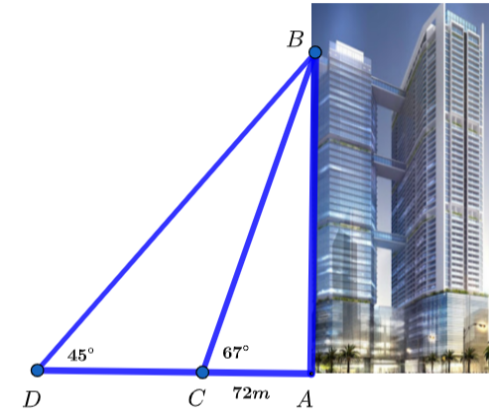
Tháp chung cư cư Discovery Complex A với quy mô 54 tầng, đang là tòa nhà cao nhất quận Cầu Giấy. Tại một thời điểm trong ngày, tia nắng mặt trời tạo với mặt đất một góc xấp xỉ 67° và bóng của tòa nhà trên mặt đất dài khoảng 72 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. 240 m.
B. 170 m.
C. 107 m.
D. 172 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập