Nghiên cứu số bệnh nhân trong một viện bỏng, thấy rằng có 2 nguyên nhân gây ra bỏng là bỏng nhiệt và bỏng do hóa chất. Bỏng nhiệt chiếm 70% số bệnh nhân và bỏng do hóa chất là 30%. Trong những bệnh nhân bị bỏng nhiệt thì có 30% bị biến chứng, trong những bệnh nhân bị bỏng hóa chất thì có 50% bị biến chứng. Rút ngẫu nhiên một bệnh án của một bệnh nhân.
a) Xác suất lấy được bệnh án của bệnh nhân bị bỏng hóa chất là 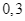 .
.
b) Xác suất lấy được bệnh án của bệnh nhân bỏng nhiệt bị biến chứng là 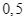 .
.
c) Xác suất lấy được bệnh án của bệnh nhân bị biến chứng là 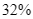 .
.
d) Biết rằng bệnh án rút ra của bệnh nhân bị biến chứng, xác suất bệnh án đó là của bệnh nhân bị bỏng nhiệt là 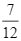 .
.
Nghiên cứu số bệnh nhân trong một viện bỏng, thấy rằng có 2 nguyên nhân gây ra bỏng là bỏng nhiệt và bỏng do hóa chất. Bỏng nhiệt chiếm 70% số bệnh nhân và bỏng do hóa chất là 30%. Trong những bệnh nhân bị bỏng nhiệt thì có 30% bị biến chứng, trong những bệnh nhân bị bỏng hóa chất thì có 50% bị biến chứng. Rút ngẫu nhiên một bệnh án của một bệnh nhân.
a) Xác suất lấy được bệnh án của bệnh nhân bị bỏng hóa chất là ![]() .
.
b) Xác suất lấy được bệnh án của bệnh nhân bỏng nhiệt bị biến chứng là ![]() .
.
c) Xác suất lấy được bệnh án của bệnh nhân bị biến chứng là ![]() .
.
d) Biết rằng bệnh án rút ra của bệnh nhân bị biến chứng, xác suất bệnh án đó là của bệnh nhân bị bỏng nhiệt là ![]() .
.
Quảng cáo
Trả lời:
Gọi ![]() là biến cố “bệnh án rút ra của bệnh nhân bị biến chứng”.
là biến cố “bệnh án rút ra của bệnh nhân bị biến chứng”.
Gọi ![]() là biến cố “bệnh án rút ra của bệnh nhân bị bỏng nhiệt”.
là biến cố “bệnh án rút ra của bệnh nhân bị bỏng nhiệt”.
Khi đó ![]() là biến cố “bệnh án rút ra của bệnh nhân bị bỏng hóa chất”.
là biến cố “bệnh án rút ra của bệnh nhân bị bỏng hóa chất”.
Theo đề:
Xác suất do bị bỏng nhiệt là: ![]() .
.
Xác suất bị biến chứng trong bỏng nhiệt là ![]()
![]() .
.
Xác suất do bị bỏng hóa chất là ![]() nên a) đúng.
nên a) đúng.
Xác suất bị biến chứng trong bỏng hóa chất là ![]()
![]() nên b) đúng.
nên b) đúng.
c) Sai. Xác suất biến cố “bệnh án rút ra của bệnh nhân bị biến chứng”:
![]() .
.
d) Đúng. Xác suất bệnh án rút ra là của bệnh nhân bị biến chứng do bỏng nhiệt:
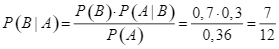 .
.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 9,3.
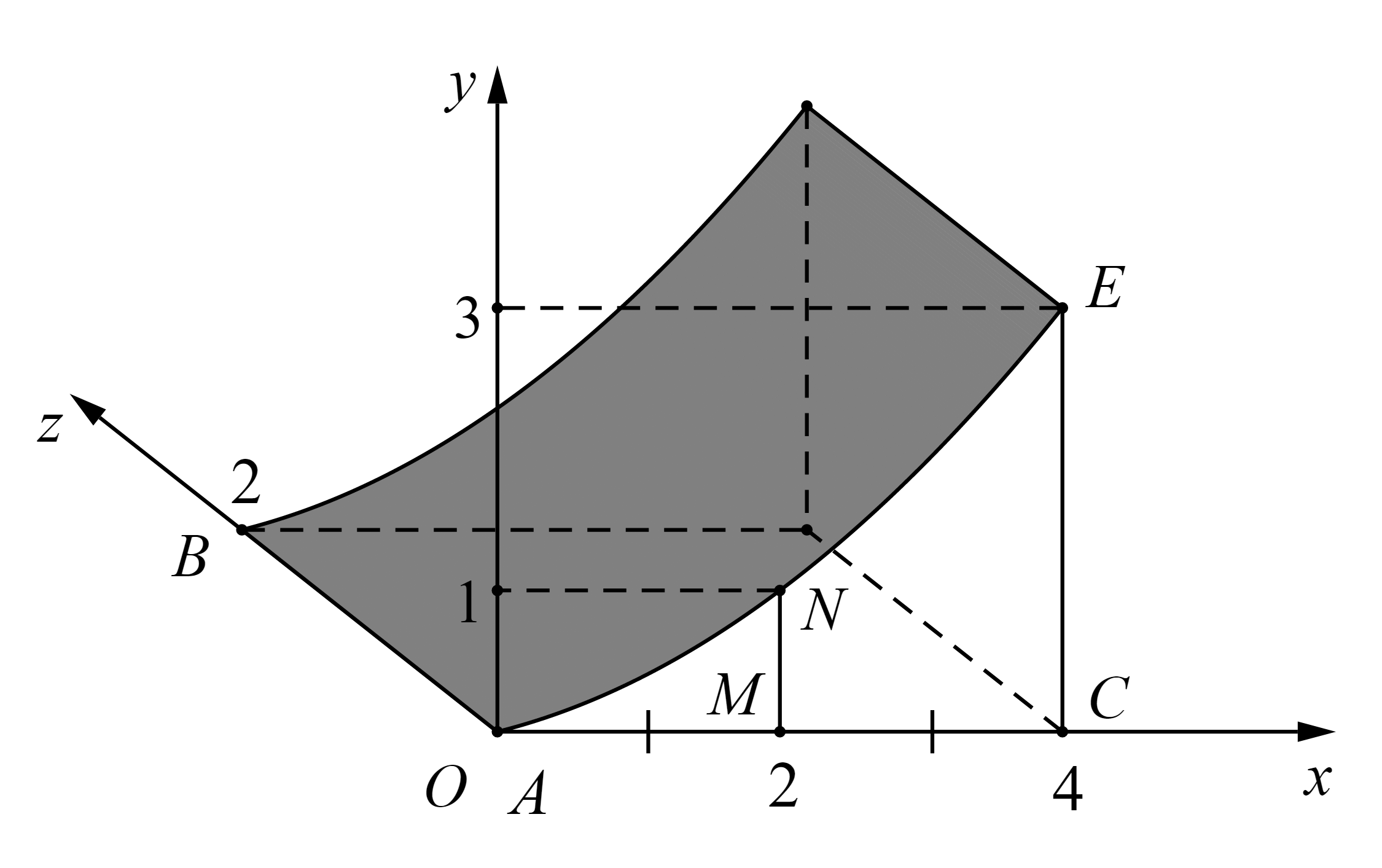
Chọn hệ tọa độ ![]() sao cho: Gốc tọa độ
sao cho: Gốc tọa độ ![]() trùng với điểm
trùng với điểm ![]() , tia
, tia ![]() trùng với tia
trùng với tia ![]() , tia
, tia ![]() cùng hướng với vectơ
cùng hướng với vectơ ![]() , tia
, tia ![]() trùng với tia
trùng với tia ![]() .
.
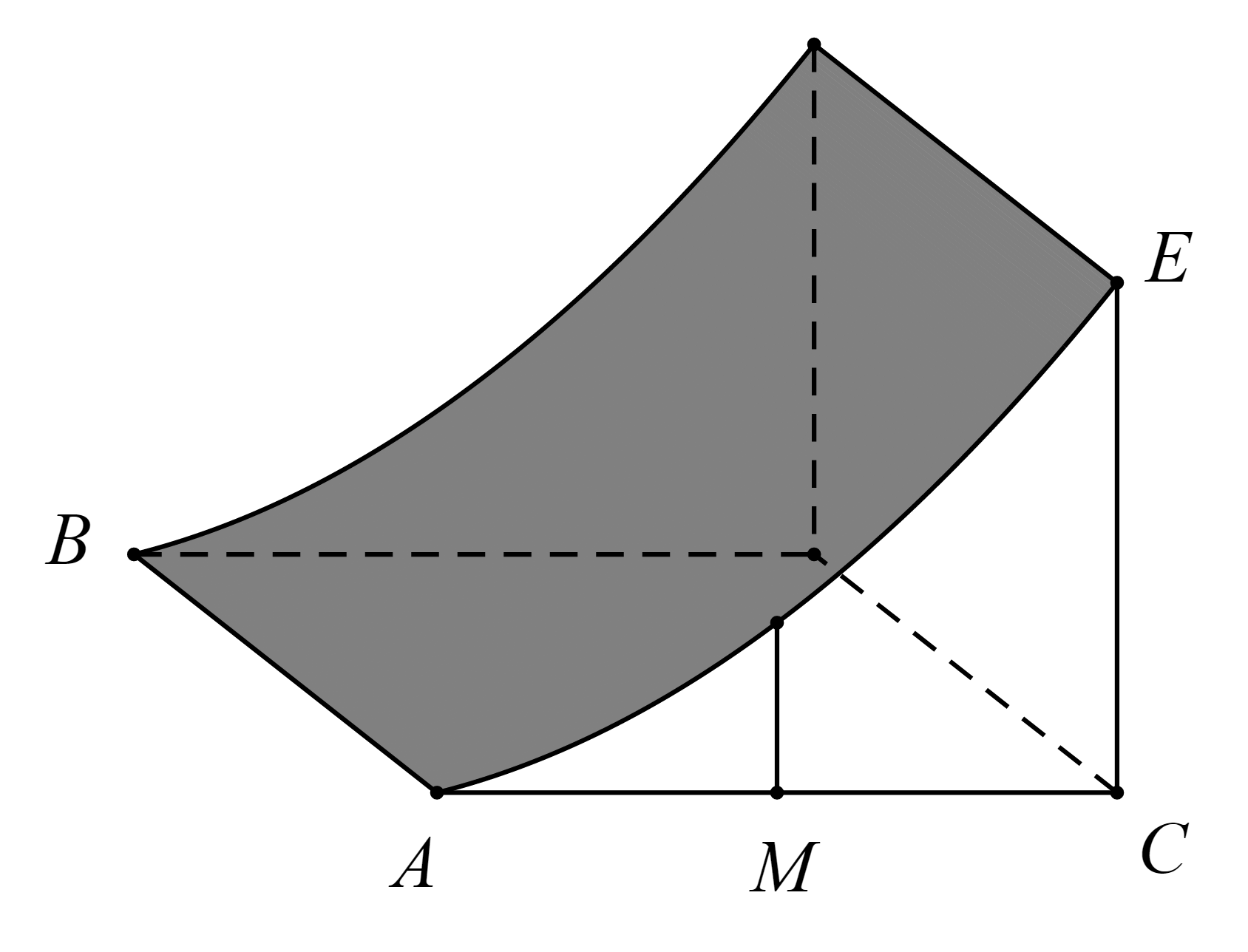
Gọi ![]() là điểm trên cạnh cong
là điểm trên cạnh cong ![]() và cách mặt đất
và cách mặt đất ![]() m.
m.
Xét mặt phẳng ![]() : Với cách chọn hệ tọa độ như trên, ta có
: Với cách chọn hệ tọa độ như trên, ta có ![]() ,
, ![]() và
và ![]() .
.
Gọi phương trình của cạnh cong ![]() (là parabol) có dạng
(là parabol) có dạng ![]() .
.
Vì parabol đi qua ba điểm ![]() ,
, ![]() và
và ![]() nên ta có hệ phương trình
nên ta có hệ phương trình  .
.
Suy ra phương trình của parabol là ![]() .
.
Vì khi cắt tường cong bởi mặt phẳng vuông góc với ![]() tại điểm có hoành độ
tại điểm có hoành độ ![]()
![]() thì ta được thiết diện là hình chữ nhật có diện tích bằng
thì ta được thiết diện là hình chữ nhật có diện tích bằng ![]() nên thể tích của tường cong là
nên thể tích của tường cong là 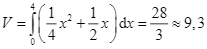
![]() .
.
Lời giải
Đáp án: 39.
Gọi cạnh đáy và chiều cao của cabin lần lượt là ![]() .
.
Theo bài ra ta có: 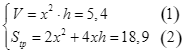 .
.
Từ ![]() suy ra
suy ra ![]() , thế vào
, thế vào ![]() ta được
ta được ![]() .
.
Khi đó, ![]() m. Vậy khoang cabin có cạnh đáy bằng 150 cm; chiều cao bằng 240 cm.
m. Vậy khoang cabin có cạnh đáy bằng 150 cm; chiều cao bằng 240 cm.
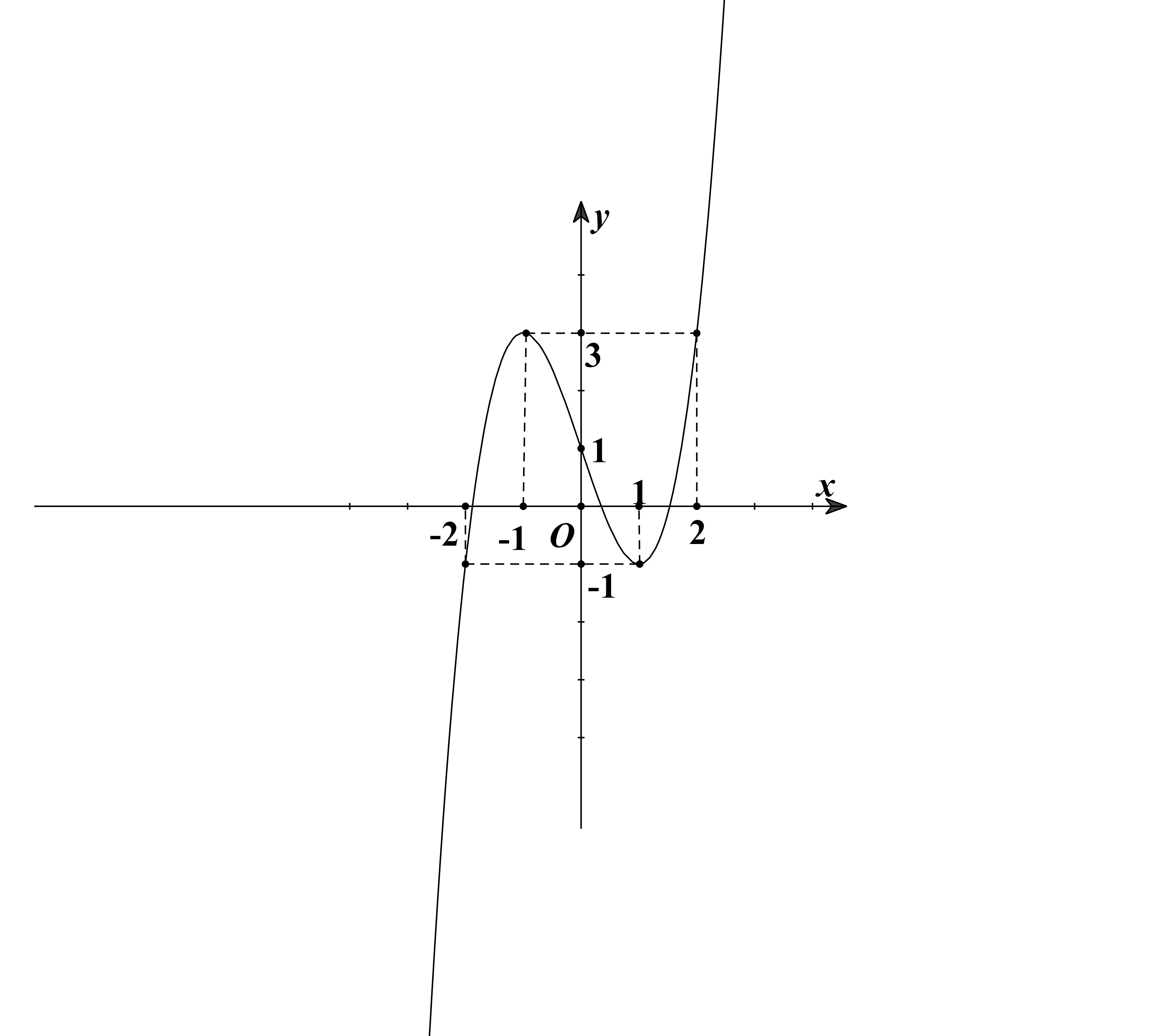
Từ giả thiết ![]() có 3 tọa độ đều dương và
có 3 tọa độ đều dương và ![]() cách mặt phẳng
cách mặt phẳng ![]() một đoạn bằng 24 đơn vị, cách mặt phẳng
một đoạn bằng 24 đơn vị, cách mặt phẳng ![]() một đoạn bằng 1 đơn vị, cách mặt phẳng
một đoạn bằng 1 đơn vị, cách mặt phẳng ![]() một đoạn bằng 14 đơn vị.
một đoạn bằng 14 đơn vị.
Do đó, ![]() . Vậy tổng các tọa độ của điểm
. Vậy tổng các tọa độ của điểm ![]() bằng
bằng ![]() .
.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.