Xác suất để công ty  thuê một trong hai công ty vệ tinh
thuê một trong hai công ty vệ tinh 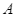 và
và 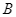 tư vấn lần lượt là
tư vấn lần lượt là 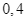 và
và 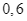 . Theo kinh nghiệm khả năng
. Theo kinh nghiệm khả năng 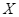 phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn của công ty
phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn của công ty 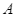 và
và 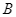 lần lượt là
lần lượt là 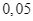 và
và 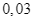 .
.
a) Xác suất để 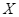 có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn là
có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn là 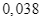 .
.
b) Biết 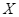 có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn. Xác suất để
có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn. Xác suất để 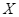 thuê công ty
thuê công ty 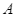 tư vấn là
tư vấn là 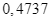 .
.
c) Biết 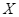 có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn. Xác suất để
có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn. Xác suất để 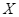 thuê công ty
thuê công ty 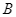 tư vấn là
tư vấn là 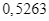 .
.
d) Biết 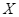 không phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn. Xác suất để
không phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn. Xác suất để 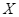 thuê công ty
thuê công ty 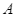 tư vấn là
tư vấn là 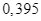 .
.
Xác suất để công ty ![]() thuê một trong hai công ty vệ tinh
thuê một trong hai công ty vệ tinh ![]() và
và ![]() tư vấn lần lượt là
tư vấn lần lượt là ![]() và
và ![]() . Theo kinh nghiệm khả năng
. Theo kinh nghiệm khả năng ![]() phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn của công ty
phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn của công ty ![]() và
và ![]() lần lượt là
lần lượt là ![]() và
và ![]() .
.
a) Xác suất để ![]() có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn là
có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn là ![]() .
.
b) Biết ![]() có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn. Xác suất để
có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn. Xác suất để ![]() thuê công ty
thuê công ty ![]() tư vấn là
tư vấn là ![]() .
.
c) Biết ![]() có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn. Xác suất để
có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn. Xác suất để ![]() thuê công ty
thuê công ty ![]() tư vấn là
tư vấn là ![]() .
.
d) Biết ![]() không phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn. Xác suất để
không phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn. Xác suất để ![]() thuê công ty
thuê công ty ![]() tư vấn là
tư vấn là ![]() .
.
Quảng cáo
Trả lời:
a) Đúng. Xét các biến cố:
![]() : “Công ty
: “Công ty ![]() thuê công ty vệ tinh
thuê công ty vệ tinh ![]() tư vấn”;
tư vấn”;
![]() : “Công ty
: “Công ty ![]() có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn”.
có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn”.
Ta có ![]() , do đó
, do đó ![]() là biến cố: “Công ty
là biến cố: “Công ty ![]() thuê công ty vệ tinh
thuê công ty vệ tinh ![]() tư vấn”.
tư vấn”.
Theo bài ra, ta có: ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Áp dụng công thức xác suất toàn phần, ta có:
![]() .
.
Vậy xác suất để ![]() có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn là
có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn là ![]() .
.
b) Sai. Theo công thức Bayes, ta có 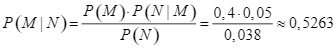 .
.
Vậy khi biết ![]() có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn thì xác suất để
có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn thì xác suất để ![]() thuê công ty
thuê công ty ![]() tư vấn khoảng
tư vấn khoảng ![]() .
.
c) Sai. Tương tự ý b), ta có 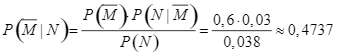 .
.
Vậy khi biết ![]() có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn thì xác suất để
có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn thì xác suất để ![]() thuê công ty
thuê công ty ![]() tư vấn khoảng
tư vấn khoảng ![]() .
.
Cách khác: Ta có thể sử dụng công thức ![]() .
.
Suy ra ![]() .
.
d) Đúng. ![]() là biến cố: “Công ty
là biến cố: “Công ty ![]() không phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn”.
không phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn”.
Khi đó, ![]() .
.
Ta cũng có ![]() .
.
Áp dụng công thức Bayes, ta có: 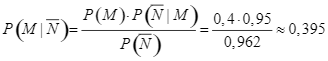 .
.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: ![]() .
.
Gọi ![]() là biến cố: “An lấy ra viên bi màu xanh”.
là biến cố: “An lấy ra viên bi màu xanh”.
Khi đó ![]() là một hệ đầy đủ các biến cố với
là một hệ đầy đủ các biến cố với ![]() .
.
Gọi ![]() là biến cố: “Tất cả các viên bi được hai bạn chọn ra đều có đủ cả hai màu”.
là biến cố: “Tất cả các viên bi được hai bạn chọn ra đều có đủ cả hai màu”.
Ta có ![]() chính là xác suất 2 viên bi Bình lấy ra có ít nhất một viên bi màu đỏ, do đó
chính là xác suất 2 viên bi Bình lấy ra có ít nhất một viên bi màu đỏ, do đó
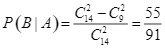 .
.
Tương tự ![]() chính là xác suất 3 viên bi Bình lấy ra có ít nhất một viên bi màu xanh, do đó
chính là xác suất 3 viên bi Bình lấy ra có ít nhất một viên bi màu xanh, do đó
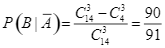 .
.
Áp dụng công thức xác suất Bayes, ta có:
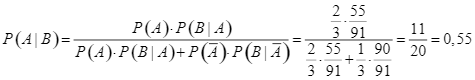 .
.
Lời giải
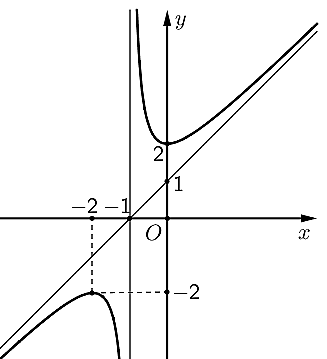
a) Sai. Nhìn đồ thị ta thấy hàm số nghịch biến trên các khoảng ![]() và
và ![]() .
.
b) Đúng. Nhìn đồ thị ta thấy đồ thị hàm số có đường tiệm cận xiên đi qua hai điểm ![]() nên có phương trình:
nên có phương trình: ![]() .
.
c) Sai. Nhìn đồ thị ta thấy đồ thị hàm số có hai điểm cực trị là ![]() . Khi đó diện tích của tam giác
. Khi đó diện tích của tam giác ![]() bằng:
bằng: ![]() .
.
d) Đúng. Đồ thị hàm số có hai đường tiệm cận là ![]() . Trục đối xứng của đồ thị hàm số là hai đường phân giác của góc tạo bởi hai đường tiệm cận.
. Trục đối xứng của đồ thị hàm số là hai đường phân giác của góc tạo bởi hai đường tiệm cận.
Giao điểm của hai đường tiệm cận là ![]() ; ta lấy
; ta lấy ![]() .
.
Xác định điểm ![]() sao cho:
sao cho: ![]() .
.
+ Trường hợp 1: ![]() , khi đó phân giác của góc tạo bởi hai đường tiệm cận của đồ thị hàm số sẽ đi qua điểm
, khi đó phân giác của góc tạo bởi hai đường tiệm cận của đồ thị hàm số sẽ đi qua điểm ![]() và có vectơ pháp tuyến là
và có vectơ pháp tuyến là ![]() nên có phương trình là
nên có phương trình là ![]() .
.
+ Trường hợp 2: ![]() , khi đó phân giác của góc tạo bởi hai đường tiệm cận của đồ thị hàm số sẽ đi qua điểm
, khi đó phân giác của góc tạo bởi hai đường tiệm cận của đồ thị hàm số sẽ đi qua điểm ![]() và có vectơ pháp tuyến là
và có vectơ pháp tuyến là ![]() nên có phương trình là
nên có phương trình là 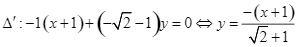 .
.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
PHẦN III. Câu trắc nghiệm trả lời ngắn.
Trong một cuộc thi về “bữa ăn dinh dưỡng”, ban tổ chức yêu cầu để đảm bảo lượng dinh dưỡng hằng ngày thì mỗi gia đình có 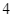 thành viên cần ít nhất
thành viên cần ít nhất 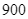 đơn vị protein và
đơn vị protein và 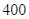 đơn vị lipid trong thức ăn hằng ngày. Mỗi kilôgam thịt bò chứa
đơn vị lipid trong thức ăn hằng ngày. Mỗi kilôgam thịt bò chứa 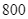 đơn vị protein và
đơn vị protein và 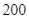 đơn vị lipid, mỗi kilôgam thịt heo chứa
đơn vị lipid, mỗi kilôgam thịt heo chứa 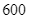 đơn vị protein và
đơn vị protein và 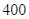 đơn vị lipid. Biết rằng người nội trợ chỉ được chi tối đa
đơn vị lipid. Biết rằng người nội trợ chỉ được chi tối đa 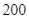 ngàn đồng để mua thịt. Biết rằng 1 kg thịt bò giá
ngàn đồng để mua thịt. Biết rằng 1 kg thịt bò giá 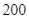 nghìn đồng, 1 kg thịt heo giá
nghìn đồng, 1 kg thịt heo giá 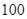 nghìn đồng. Người nội trợ nên mua
nghìn đồng. Người nội trợ nên mua 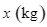 thịt bò và
thịt bò và 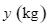 thịt heo để phí thấp nhất cho khẩu phần thức ăn mà vẫn đảm bảo chất dinh dưỡng, khi đó hãy tìm
thịt heo để phí thấp nhất cho khẩu phần thức ăn mà vẫn đảm bảo chất dinh dưỡng, khi đó hãy tìm  .
.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.