Một miếng đất hình chữ nhật có chiều dài hơn chiều rộng \(25{\rm{ m}}\). Nếu giảm chiều dài đi \(25{\rm{ m}}\) thì diện tích sẽ nhỏ hơn diện tích ban đầu là \(1{\rm{ }}000{\rm{ }}{{\rm{m}}^2}\). Gọi chiều dài ban đầu của miếng dất là \(x\) \(\left( {x > 25,{\rm{ m}}} \right).\)
a) Chiều rộng ban đầu của miếng đất là \(x - 25{\rm{ }}\left( {\rm{m}} \right)\).
b) Khi chiều dài giảm đi \(25{\rm{ m}}\)ta được chiều dài mới bằng chiều rộng ban đầu của mảnh đất.
c) Phương trình mô tả bài toán là \(x\left( {x - 25} \right) - \left( {x - 25} \right)\left( {x - 25} \right) = 1{\rm{ }}000\).
d) Diện tích ban đầu của mảnh đất là \({\rm{2 600 }}\left( {{{\rm{m}}^2}} \right)\).
Một miếng đất hình chữ nhật có chiều dài hơn chiều rộng \(25{\rm{ m}}\). Nếu giảm chiều dài đi \(25{\rm{ m}}\) thì diện tích sẽ nhỏ hơn diện tích ban đầu là \(1{\rm{ }}000{\rm{ }}{{\rm{m}}^2}\). Gọi chiều dài ban đầu của miếng dất là \(x\) \(\left( {x > 25,{\rm{ m}}} \right).\)
a) Chiều rộng ban đầu của miếng đất là \(x - 25{\rm{ }}\left( {\rm{m}} \right)\).
b) Khi chiều dài giảm đi \(25{\rm{ m}}\)ta được chiều dài mới bằng chiều rộng ban đầu của mảnh đất.
c) Phương trình mô tả bài toán là \(x\left( {x - 25} \right) - \left( {x - 25} \right)\left( {x - 25} \right) = 1{\rm{ }}000\).
d) Diện tích ban đầu của mảnh đất là \({\rm{2 600 }}\left( {{{\rm{m}}^2}} \right)\).
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng là: a) Đ b) Đ c) Đ d) Đ
Gọi chiều dài ban đầu của miếng dất là \(x\) \(\left( {x > 25,{\rm{ m}}} \right).\)
Chiều rộng ban đầu của miếng đất là \(x - 25{\rm{ }}\left( {\rm{m}} \right)\).
Chiều dài của miếng dất sau khi giảm là \(x - 25{\rm{ }}\left( {\rm{m}} \right)\).
Diện tích ban đầu của mảnh đất là: \(x\left( {x - 25} \right){\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
Diện tích sau khi giảm chiều dài của mảnh đất là: \(\left( {x - 25} \right)\left( {x - 25} \right){\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
Theo đề, diện tích sau khi giảm sẽ nhỏ hơn diện tích ban đầu là \(1{\rm{ }}000{\rm{ }}{{\rm{m}}^2}\) nên ta có phương trình:
\(x\left( {x - 25} \right) - \left( {x - 25} \right)\left( {x - 25} \right) = 1{\rm{ 000 }}\left( {{{\rm{m}}^2}} \right)\)
Giải phương trình, ta có:
\(x\left( {x - 25} \right) - \left( {x - 25} \right)\left( {x - 25} \right) = 1{\rm{ 000}}\)
\({x^2} - 25x - {x^2} + 50x - 625 = 1{\rm{ 000}}\)
\(25x = 1{\rm{ }}625\)
\(x = 65\) (thỏa mãn).
Do đó, diện tích ban đầu của miếng đất là \(65.\left( {65 - 25} \right) = 2{\rm{ }}600{\rm{ }}\left( {{{\rm{m}}^{\rm{2}}}} \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là:
Gọi \(x\) là số cây đội I trồng được trong tháng trước \(\left( {0 < x < 700,{\rm{ }}x \in {\mathbb{N}^*}} \right)\).
Khi đó, số cây đội II trồng được trong tháng trước là \(700 - x\) (cây).
Số cây đội I trồng được trong tháng này là \(160\% .x = 1,6x\) (cây)
Số cây mà đội II trồng được trong tháng này là \(140\% \left( {700 - x} \right) = 980 - 1,4x\).
Theo đề, tháng này cả hai đội trồng được \(1{\rm{ }}100\) cây, do đó ta có phương trình:
\(1,6x + 980 - 1,4x = 1{\rm{ }}100\)
Giải phương trình, ta được:
\(1,6x + 960 - 1,4x = 1{\rm{ }}100\)
\(980 + 0,2x = 1{\rm{ }}100\)
\(0,2x = 1{\rm{ }}100 - 980\)
\(0,2x = 120\)
\(x = 600\) (thỏa mãn)
Vậy tháng trước đội I trồng được \(600\) cây, đội II trồng được \(100\) cây.
Lời giải
Hướng dẫn giải
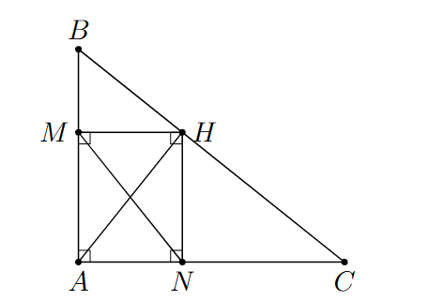
a) Áp dụng định lí Pythagore vào \(\Delta ABC\), ta có:
\(A{B^2} + A{C^2} = B{C^2}\)
\({6^2} + {8^2} = B{C^2}\)
\(B{C^2} = 100\) nên \(BC = 10{\rm{ cm}}\).
b) Xét \(\Delta ABH\) và \(\Delta CAB\) có \(\widehat {BAC} = \widehat {AHB} = 90^\circ \) và \(\widehat {ABC} = \widehat {ABH}\) (góc chung)
Suy ra (g.g)
Suy ra \(\frac{{AH}}{{CB}} = \frac{{AB}}{{CA}}\) hay \(AH.BC = AB.AC\).
Từ giả thiết, ta có: \(\widehat {CAB} = \widehat {HMA} = \widehat {HNA} = 90^\circ \) nên \(AMHN\) là hình chữ nhật.
Do \(AMHN\) là hình chữ nhật nên ta có \(\widehat {ANM} = \widehat {AHM}\) (so le trong)
Mặt khác \(\widehat {AHM} = \widehat {ABC}\) (cùng phụ với \(\widehat {HAB}\))
Suy ra \(\widehat {ANM} = \widehat {ABC}\)
Xét \(\Delta AMN\) và \(\Delta ACB\) có: \(\widehat {MAN} = \widehat {BAC} = 90^\circ \) và \(\widehat {ANM} = \widehat {ABC}\) (cmt)
Suy ra (g.g)
c) Do nên ta có: \(\frac{{{S_{ANM}}}}{{{S_{ABC}}}} = \frac{{M{N^2}}}{{B{C^2}}} = \frac{{A{H^2}}}{{B{C^2}}}\)
(do \(AMHN\) là hình chữ nhật nên \(AH = MN\)).
Ta có: \({S_{ABC}} = \frac{1}{2}AB.AC = 24{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).
Lại có, \(AH.BC = AB.AC\) nên \(AH = \frac{{AB.AC}}{{BC}} = \frac{{6.8}}{{10}} = 4,8\) cm.
Do đó, \(\frac{{{S_{ANM}}}}{{{S_{ABC}}}} = \frac{{A{H^2}}}{{B{C^2}}} = \frac{{4,{8^2}}}{{{{10}^2}}} = 0,2304\) suy ra \({S_{ANM}} = 0,2304.{S_{ABC}} = 5,5296{\rm{ c}}{{\rm{m}}^2}\).
Ta có: \({S_{ANM}} + {S_{BMNC}} = {S_{ABC}}\) nên \({S_{BMNC}} = {S_{ABC}} - {S_{AMN}} = 24 - 5,5296 = 18,4704{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).
Vậy \({S_{BMNC}} = 18,4704{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
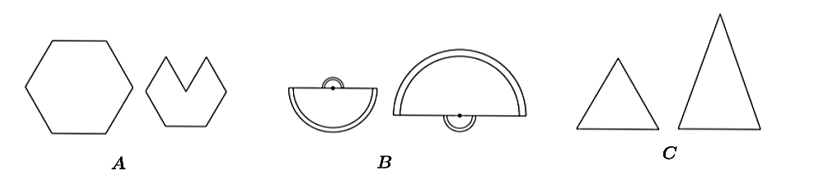
A. Hình \(A\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.