Câu hỏi:
15/02/2025 149
Cho \(\Delta ABC\) có các đường trung tuyến \(BD,CE\). Gọi \(M,N\) theo thứ tự là trung điểm của \(BE,CD\). Gọi \(I,K\) theo thứ tự là giao điểm của \(MN\) với \(BD\) và \(CE\). Chứng minh rằng:
a) \(DE\parallel BC\).
b) \(MN\parallel BC.\)
c) \(MI = IK = KN.\)
Cho \(\Delta ABC\) có các đường trung tuyến \(BD,CE\). Gọi \(M,N\) theo thứ tự là trung điểm của \(BE,CD\). Gọi \(I,K\) theo thứ tự là giao điểm của \(MN\) với \(BD\) và \(CE\). Chứng minh rằng:
a) \(DE\parallel BC\).
b) \(MN\parallel BC.\)
c) \(MI = IK = KN.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
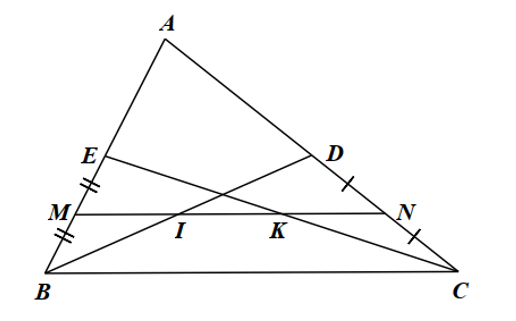
a) Trong \(\Delta ABC\) có các đường trung tuyến \(BD,CE\) nên \(D\) là trung điểm của \(AC\), \(E\) là trung điểm của \(AB\) nên \(ED\) là đường trung bình của \(\Delta ABC\).
Suy ra \(ED = \frac{1}{2}BD\) và \(ED\parallel BC\) (tính chất đường trung bình của tam giác)
b) Ta có: \(E\) là trung điểm của \(AB\) nên \(AE = EB = \frac{1}{2}AB.\)
Mà \(M\) là trung điểm của \(EB\) nên \(EM = MB = \frac{1}{2}EB = \frac{1}{4}AB\) hay \(\frac{{MB}}{{AB}} = \frac{1}{4}\).
Lại có \(N\) là trung điểm của \(CD\) nên \(NC = DN = \frac{1}{2}DC = \frac{1}{4}AC\) hay \(\frac{{NC}}{{AC}} = \frac{1}{4}\).
Suy ra \(\frac{{MB}}{{AB}} = \frac{{NC}}{{AC}} = \frac{1}{4}\).
Xét \(\Delta ABC\) có \(\frac{{MB}}{{AB}} = \frac{{NC}}{{AC}}\) nên \(MN\parallel BC\) (định lí Thalès đảo).
c) Ta có \(MN\parallel BC\) (câu b) và \(ED\parallel BC\) (câu a) nên \(ED\parallel MN\parallel BC\).
Xét \(\Delta BDE\) có \(M\) là trung điểm của \(EB\) và \(MI\parallel ED\) (do \(ED\parallel MN\parallel BC\)).
Suy ra \(I\) là trung điểm của \(BD\) hay \(IB = ID\).
Khi đó \(MI\) là đường trung bình của \(\Delta BDE\) nên \(MI = \frac{1}{2}ED\).
Xét \(\Delta CDE\) ta cũng có \(N\) là trung điểm của \(CD\) và \(NK\parallel ED\) (do \(ED\parallel MN\parallel BC\))
Suy ra \(K\) là trung điểm của \(EC\) hay \(EK = KC\).
Khi đó, \(KN\) là đường trung bình của \(\Delta CDE\) nên \(NK = \frac{1}{2}ED\), trong \(\Delta CBE\) có \(MK = \frac{1}{2}BC\).
Ta có: \(IK = MK - MI = \frac{1}{2}BC - \frac{1}{2}ED = ED - \frac{1}{2}DE = \frac{1}{2}DE\).
Do đó, \(MI = IK = KN.\)
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: a) Đ b) S c) S d) S
Gọi \(x\) (giờ) là thời gian từ lúc xe con đi tới đuổi kịp xe khách (\(x > 0\)).
Thời gian xe khách đi tới lúc gặp xe con là \(x + 3\) (giờ).
Quãng đường đi được của xe con là \(50x\) (km).
Quãng đường đi được của xe khách là \(20\left( {x + 3} \right)\) (km).
Theo đề, ta có phương trình \(20\left( {x + 3} \right) = 50x\).
Giải phương trình, ta được:
\(20\left( {x + 3} \right) = 50x\)
\(20x + 60 = 50x\)
\(50x - 20x = 60\)
\(30x = 60\)
\(x = 2\) (thỏa mãn).
Vậy sau \(2\) giờ thì xe con đuổi kịp xe khách.
Lời giải
Đáp án đúng là: A
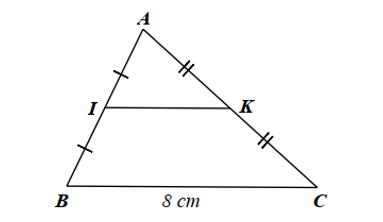
Xét \(\Delta ABC\) có \(I,K\) lần lượt là trung điểm của \(AB,AC\) nên \(IK\) là đường trung bình của tam giác.
Do đó, \(IK = \frac{1}{2}BC\) suy ra \(IK = 4{\rm{ cm}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Dạng 1: Bài luyện tập 1 dạng 1: Tính có đáp án
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 24
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Đề cuối kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 1
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 2)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận