Câu hỏi:
16/02/2025 259
Cho hàm số \(y = \left( {m - 1} \right)x + m\) \((m\) là tham số \(m \ne 1)\) có đồ thị là đường thẳng \(\left( d \right).\)
a) Tìm \(m\) để \(\left( d \right):y = \left( {m - 1} \right)x + m\) song song với \(\left( {d'} \right):y = 2x - 3.\)
b) Vẽ \(\left( d \right)\) với \(m\) tìm được và vẽ \(\left( {d'} \right)\) trên cùng mặt phẳng tọa độ \(Oxy.\)
c) Tìm \(m\) để đường thẳng \(\left( d \right):y = \left( {m - 1} \right)x + m\) và hai đường thẳng \(y = x + 2;\,\,y = \frac{1}{2}x + 3\) đồng quy.
Cho hàm số \(y = \left( {m - 1} \right)x + m\) \((m\) là tham số \(m \ne 1)\) có đồ thị là đường thẳng \(\left( d \right).\)
a) Tìm \(m\) để \(\left( d \right):y = \left( {m - 1} \right)x + m\) song song với \(\left( {d'} \right):y = 2x - 3.\)
b) Vẽ \(\left( d \right)\) với \(m\) tìm được và vẽ \(\left( {d'} \right)\) trên cùng mặt phẳng tọa độ \(Oxy.\)
c) Tìm \(m\) để đường thẳng \(\left( d \right):y = \left( {m - 1} \right)x + m\) và hai đường thẳng \(y = x + 2;\,\,y = \frac{1}{2}x + 3\) đồng quy.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Với \(m \ne 1,\) để đường thẳng \(\left( d \right):y = \left( {m - 1} \right)x + m\) song song với đường thẳng \(\left( {d'} \right):y = 2x - 3\) thì \(m - 1 = 2\) và \(m \ne - 3,\) tức là \(m = 3\) (thỏa mãn \(m \ne 1,\,\,m \ne - 3).\)
Vậy \(m = 3.\)
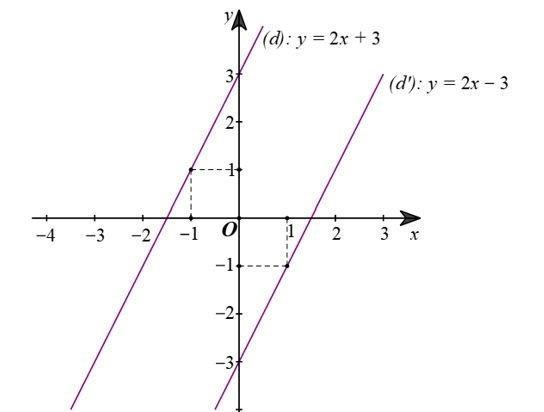
b) ⦁ Với \(m = 3,\) ta có hàm số \(y = 2x + 3.\)
Cho \(x = 0,\) ta có \(y = 3.\)
Cho \(x = - 1,\) ta có \(y = 1.\)
Đồ thị hàm số \(y = 2x + 3\) là đường thẳng \(\left( d \right)\) đi qua hai điểm \(\left( {0;3} \right)\) và \(\left( { - 1;1} \right).\)
⦁ Xét hàm số \(y = 2x - 3.\)\(y = - 3.\)
Cho \(x = 0,\) ta có
Cho \(x = 1,\) ta có \(y = - 1.\)
Đồ thị hàm số \(y = 2x - 3\) là đường thẳng \(\left( {d'} \right)\) đi qua hai điểm \(\left( {0; - 3} \right)\) và \(\left( {1; - 1} \right).\)
c) Gọi \(A\left( {{x_A};\,\,{y_A}} \right)\) là giao điểm của hai đường thẳng \(y = x + 2;y = \frac{1}{2}x + 3.\)
Vì \(A\) thuộc đường thẳng \(y = x + 2\) nên ta có \({y_A} = {x_A} + 2.\) Khi đó \(A\left( {{x_A};\,\,{x_A} + 2} \right).\)
Vì \(A\) thuộc đường thẳng \(y = \frac{1}{2}x + 3\) nên ta có \({x_A} + 2 = \frac{1}{2}{x_A} + 3,\) suy ra \(\frac{1}{2}{x_A} = 1,\) do đó \({x_A} = 2.\)
Từ đó ta có \({y_A} = {x_A} + 2 = 2 + 2 = 4.\)
Vì vậy ta được \(A\left( {2;4} \right).\)
Để ba đường thẳng \(y = x + 2;y = \frac{1}{2}x + 3\) và \(\left( d \right):y = \left( {m - 1} \right)x + m\) đồng quy thì đường thẳng \(\left( d \right)\) phải đi qua giao điểm \(A\left( {2;4} \right)\) của hai đường thẳng \(y = x + 2;y = \frac{1}{2}x + 3.\)
Khi đó \(x = 2,\,\,y = 4\) thỏa mãn hàm số \(y = \left( {m - 1} \right)x + m,\) ta được:
\(4 = \left( {m - 1} \right) \cdot 2 + m,\) suy ra \(2m - 2 + m = 4,\) do đó \(3m = 6,\) nên \(m = 2\) (thỏa mãn \(m \ne 1).\)
Vậy \(m = 2.\)
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
a) Xét \(\Delta ABM\) có \(EG\,{\rm{//}}\,BM,\) theo định lí Thalès ta có: \(\frac{{BE}}{{AE}} = \frac{{MG}}{{AG}}.\) b) Xét \(\Delta DCN\) có \(BM\,{\rm{//}}\,CN,\) theo định lí Thalès ta có: \(\frac{{DN}}{{MD}} = \frac{{DC}}{{DB}}.\) Mà \(D\) là trung điểm của \(BC\) (do \(AD\) là trung tuyến của tam giác) nên \(DC = DB.\) Do đó \(\frac{{DN}}{{MD}} = \frac{{DC}}{{DB}} = 1,\) nên \(DM = DN.\) |
 |
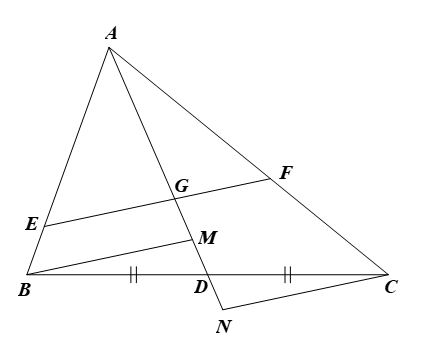Suy ra \(GM + GN = GM + GM + MN = 2GM + 2MD = 2GD.\)
Lại có \(G\) là trọng tâm \(\Delta ABC\) nên \(AG = 2GD.\)
Xét \(\Delta ACN\) có \(FG\,{\rm{//}}\,CN,\) theo định lí Thalès ta có: \(\frac{{CF}}{{AF}} = \frac{{GN}}{{AG}}.\)
Suy ra \(\frac{{BE}}{{AE}} + \frac{{CF}}{{AF}} = \frac{{MG}}{{AG}} + \frac{{GN}}{{AG}} = \frac{{GM + GN}}{{AG}} = \frac{{2GD}}{{2GD}} = 1.\)
c) Xét \(\Delta ABM\) có \(EG\,{\rm{//}}\,BM,\) theo định lí Thalès ta có: \(\frac{{AB}}{{AE}} = \frac{{AM}}{{AG}}.\)
Xét \(\Delta ACN\) có \[FG\,{\rm{//}}\,CN,\] theo định lí Thalès ta có: \(\frac{{AC}}{{AF}} = \frac{{AN}}{{AG}}.\)
Suy ra \(\frac{{AB}}{{AE}} + \frac{{AC}}{{AF}} = \frac{{AM}}{{AG}} + \frac{{AN}}{{AG}}\)\( = \frac{{AG + GM + AG + GM + MN}}{{AG}}\)
\( = \frac{{2AG + 2GM + 2MD}}{{AG}}\)\( = \frac{{2AG + 2\left( {GM + MD} \right)}}{{AG}} = \frac{{2AG + 2GD}}{{AG}}\)
\( = \frac{{2AG + 2 \cdot \frac{1}{2}AG}}{{AG}} = \frac{{3AG}}{{AG}} = 3.\)
Vậy \(\frac{{AB}}{{AE}} + \frac{{AC}}{{AF}} = 3.\)
![Lúc 6 giờ sáng, bạn Hải đi xe đạp từ điểm \[A\] đến trường (tại điểm \(B)\) phải leo lên và xuống một con (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/02/blobid36-1739679343.png)
Lời giải
![Lúc 6 giờ sáng, bạn Hải đi xe đạp từ điểm \[A\] đến trường (tại điểm \(B)\) phải leo lên và xuống một con (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/02/blobid37-1739679361.png)
Thời gian để bạn Hải đi từ \[A\] đến \[C\] là: \[6\] giờ \[30\] phút \( - \,\,6\) giờ \[ = 30\] phút \[ = 0,5\] giờ.
Quãng đường mà bạn Hải đi từ \[A\] đến \[C\] trong \(0,5\) giờ với tốc độ trung bình lên dốc 4 km/h là: \[AC = {S_{A \to C}} = 4 \cdot 0,5 = 2\] (km).
Xét \(\Delta ACB\) có \[CH\] là đường phân giác của \(\widehat {ACB},\) nên ta có: \(\frac{{HA}}{{HB}} = \frac{{CA}}{{CB}}\) hay \(\frac{{0,32}}{{0,4}} = \frac{2}{{CB}}\) Suy ra \(CB = \frac{{0,4 \cdot 2}}{{0,32}} = 2,5\) (km).
Thời gian để bạn Hải đi hết quãng đường \(2,5\) km với tốc độ trung bình xuống dốc 10 km/h là: \(\frac{{2,5}}{{10}} = 0,25\) (giờ).
Như vậy, tổng thời gian bạn Hải đi từ \[A\] đến trường \[B\] là
\[0,5 + 0,25 = 0,75\] (giờ) \[ = 45\] (phút).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo