Câu hỏi:
16/02/2025 1,129
Cho \(\Delta ABC\) có \(AD\) là trung tuyến, trọng tâm \(G,\) đường thẳng đi qua \(G\) cắt các cạnh \(AB,\,\,AC\) lần l\(B,\,\,C\)ượt tại \(E,\,\,F.\) Từ kẻ các đường song song với \(EF\) cắt \(AD\) lần lượt tại \(M,\,\,N.\) Chứng minh rằng:
a) \(\frac{{BE}}{{AE}} = \frac{{MG}}{{AG}}.\) b) \(\frac{{BE}}{{AE}} + \frac{{CF}}{{AF}} = 1.\) c) \(\frac{{AB}}{{AE}} + \frac{{AC}}{{AF}} = 3.\)
Cho \(\Delta ABC\) có \(AD\) là trung tuyến, trọng tâm \(G,\) đường thẳng đi qua \(G\) cắt các cạnh \(AB,\,\,AC\) lần l\(B,\,\,C\)ượt tại \(E,\,\,F.\) Từ kẻ các đường song song với \(EF\) cắt \(AD\) lần lượt tại \(M,\,\,N.\) Chứng minh rằng:
a) \(\frac{{BE}}{{AE}} = \frac{{MG}}{{AG}}.\) b) \(\frac{{BE}}{{AE}} + \frac{{CF}}{{AF}} = 1.\) c) \(\frac{{AB}}{{AE}} + \frac{{AC}}{{AF}} = 3.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
|
a) Xét \(\Delta ABM\) có \(EG\,{\rm{//}}\,BM,\) theo định lí Thalès ta có: \(\frac{{BE}}{{AE}} = \frac{{MG}}{{AG}}.\) b) Xét \(\Delta DCN\) có \(BM\,{\rm{//}}\,CN,\) theo định lí Thalès ta có: \(\frac{{DN}}{{MD}} = \frac{{DC}}{{DB}}.\) Mà \(D\) là trung điểm của \(BC\) (do \(AD\) là trung tuyến của tam giác) nên \(DC = DB.\) Do đó \(\frac{{DN}}{{MD}} = \frac{{DC}}{{DB}} = 1,\) nên \(DM = DN.\) |
 |
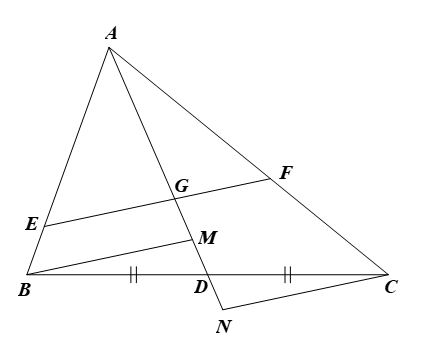Suy ra \(GM + GN = GM + GM + MN = 2GM + 2MD = 2GD.\)
Lại có \(G\) là trọng tâm \(\Delta ABC\) nên \(AG = 2GD.\)
Xét \(\Delta ACN\) có \(FG\,{\rm{//}}\,CN,\) theo định lí Thalès ta có: \(\frac{{CF}}{{AF}} = \frac{{GN}}{{AG}}.\)
Suy ra \(\frac{{BE}}{{AE}} + \frac{{CF}}{{AF}} = \frac{{MG}}{{AG}} + \frac{{GN}}{{AG}} = \frac{{GM + GN}}{{AG}} = \frac{{2GD}}{{2GD}} = 1.\)
c) Xét \(\Delta ABM\) có \(EG\,{\rm{//}}\,BM,\) theo định lí Thalès ta có: \(\frac{{AB}}{{AE}} = \frac{{AM}}{{AG}}.\)
Xét \(\Delta ACN\) có \[FG\,{\rm{//}}\,CN,\] theo định lí Thalès ta có: \(\frac{{AC}}{{AF}} = \frac{{AN}}{{AG}}.\)
Suy ra \(\frac{{AB}}{{AE}} + \frac{{AC}}{{AF}} = \frac{{AM}}{{AG}} + \frac{{AN}}{{AG}}\)\( = \frac{{AG + GM + AG + GM + MN}}{{AG}}\)
\( = \frac{{2AG + 2GM + 2MD}}{{AG}}\)\( = \frac{{2AG + 2\left( {GM + MD} \right)}}{{AG}} = \frac{{2AG + 2GD}}{{AG}}\)
\( = \frac{{2AG + 2 \cdot \frac{1}{2}AG}}{{AG}} = \frac{{3AG}}{{AG}} = 3.\)
Vậy \(\frac{{AB}}{{AE}} + \frac{{AC}}{{AF}} = 3.\)
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
![Lúc 6 giờ sáng, bạn Hải đi xe đạp từ điểm \[A\] đến trường (tại điểm \(B)\) phải leo lên và xuống một con (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/02/blobid36-1739679343.png)
Lời giải
![Lúc 6 giờ sáng, bạn Hải đi xe đạp từ điểm \[A\] đến trường (tại điểm \(B)\) phải leo lên và xuống một con (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/02/blobid37-1739679361.png)
Thời gian để bạn Hải đi từ \[A\] đến \[C\] là: \[6\] giờ \[30\] phút \( - \,\,6\) giờ \[ = 30\] phút \[ = 0,5\] giờ.
Quãng đường mà bạn Hải đi từ \[A\] đến \[C\] trong \(0,5\) giờ với tốc độ trung bình lên dốc 4 km/h là: \[AC = {S_{A \to C}} = 4 \cdot 0,5 = 2\] (km).
Xét \(\Delta ACB\) có \[CH\] là đường phân giác của \(\widehat {ACB},\) nên ta có: \(\frac{{HA}}{{HB}} = \frac{{CA}}{{CB}}\) hay \(\frac{{0,32}}{{0,4}} = \frac{2}{{CB}}\) Suy ra \(CB = \frac{{0,4 \cdot 2}}{{0,32}} = 2,5\) (km).
Thời gian để bạn Hải đi hết quãng đường \(2,5\) km với tốc độ trung bình xuống dốc 10 km/h là: \(\frac{{2,5}}{{10}} = 0,25\) (giờ).
Như vậy, tổng thời gian bạn Hải đi từ \[A\] đến trường \[B\] là
\[0,5 + 0,25 = 0,75\] (giờ) \[ = 45\] (phút).
Lời giải
a) Hàm số biểu diễn số tiền lời (hoặc lỗ) \(K\) của nhà may thu được khi bán \(t\) chiếc áo là: \(K = 300\,\,000t - 30\,\,000\,\,000\) (đồng) (với \(0 \le t \le 200).\)
Để nhà may thu hồi được vốn ban đầu thì \(K = 0,\) ta thay vào công thức\(K = 300\,\,000t - 30\,\,000\,\,000,\) ta được:
\[0 = 300\,\,000t - 30\,\,000\,\,000,\] suy ra \(t = 100.\)
Vậy cần phải bán ra được 100 chiếc áo mới thu hồi được vốn ban đầu.
b) Để nhà may lời được \(6\,\,000\,\,000\) thì \(K = 6\,\,000\,\,000,\) thay vào công thức \(K = 300\,\,000t - 30\,\,000\,\,000,\) ta được:
\(6\,\,000\,\,000 = 300\,\,000t - 30\,\,000\,\,000,\) suy ra \(t = 120.\)
Vậy cần phải bán ra được 120 chiếc áo mới lời được 6 000 000 đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Dạng 1: Bài luyện tập 1 dạng 1: Tính có đáp án
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 24
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Đề cuối kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 1
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 2)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận