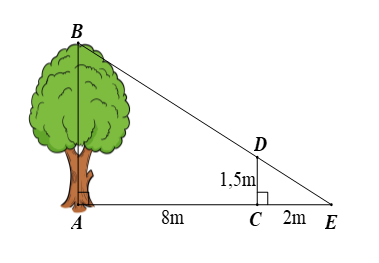
Một người cắm một cái cọc vuông góc với mặt đất sao cho bóng của đỉnh cọc trùng với bóng của ngọn cây. Biết cọc cao \[1,5\,\,{\rm{m}}\] so với mặt đất, chân cọc cách gốc cây \[8\,\,{\rm{m}}\] và cách bóng của đỉnh cọc \[2\,\,{\rm{m}}.\] Tính chiều cao của cây (kết quả làm tròn đến chữ số thập phân thứ nhất).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có \(AB \bot AE;\,\,CD \bot AE\) nên \(CD\,{\rm{//}}\,AB\).
Xét tam giác \(ABE\) có \(CD\,{\rm{//}}\,AB\), ta có
\[\,\frac{{DE}}{{AB}} = \frac{{EC}}{{EA}}\] (hệ quả của định lí Thalès).
Hay \[\frac{{1,5}}{{AB}} = \frac{2}{{2 + 8}}\] suy ra \[AB = 7,5\,\,{\rm{m}}\].
Vậy chiều cao của cây là \[7,5\,\,{\rm{m}}\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Chiều cao trung bình của trẻ 13 tuổi là: \[0,75 + 0,05 \cdot \left( {13 - 1} \right) = 1,35 \left( m \right).\]
b) Gọi \[y\] là chiều cao trung bình; \[x\] là độ tuổi của trẻ em.
Công thức mô tả sự phụ thuộc giữa chiều cao trung bình và độ tuổi của trẻ em Việt Nam là:
\[y = 0,75 + 0,25\left( {x - 1} \right).\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
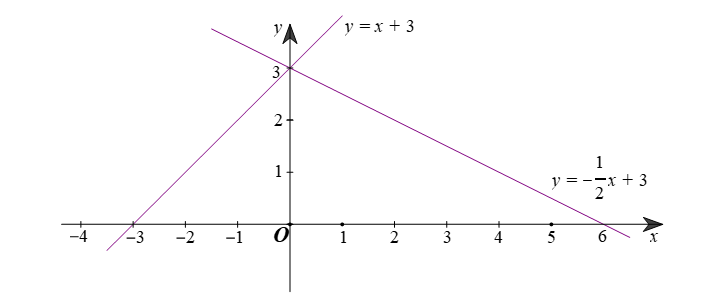
a) ⦁ Vẽ đồ thị hàm số \(y = x + 3:\)
Cho \(x = 0,\) ta có \(y = 3;\)
Cho \(y = 0,\) ta có \(x = - 3.\)
Đồ thị hàm số \(y = x + 3\) là đường thẳng đi qua hai điểm \(\left( {0;3} \right)\) và \(\left( { - 3;0} \right).\)
⦁ Vẽ đồ thị hàm số \(y = - \frac{1}{2}x + 3:\)
Cho \(x = 0,\) ta có \(y = 3;\)
Cho \(y = 0,\) ta có \(x = 6.\)
Đồ thị hàm số \(y = - \frac{1}{2}x + 3\) là đường thẳng đi qua hai điểm \(\left( {0;3} \right)\) và \(\left( {6;0} \right).\)
b)
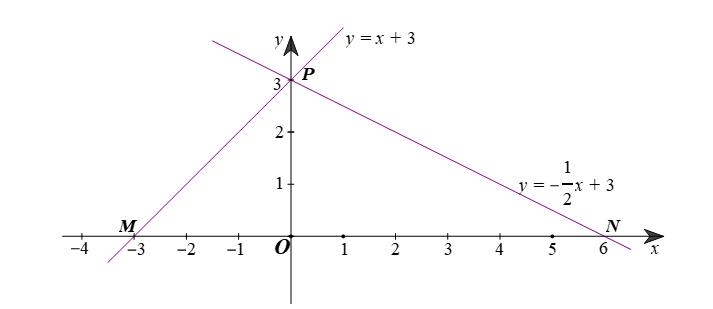
Giao điểm đồ thị của hàm số (1) với trục hoành là \(M\left( { - 3;0} \right);\)
Giao điểm đồ thị của hàm số (2) với trục hoành là \(N\left( {6;0} \right);\)
Giao điểm của hai đồ thị hàm số (1) và hàm số (2) là \(P\left( {0;3} \right).\)
Vậy \(M\left( { - 3;0} \right);\,\,N\left( {6;0} \right);\,\,P\left( {0;3} \right).\)
c) Tính độ dài các cạnh của \(\Delta MNP:\)
\(MN = MO + ON = 3 + 6 = 9{\rm{\;}}\left( {{\rm{cm}}} \right);\)
\(MP = \sqrt {M{O^2} + P{O^2}} = \sqrt {{3^2} + {3^2}} = \sqrt {18} = 3\sqrt 2 {\rm{\;}}\left( {{\rm{cm}}} \right);\)
\(NP = \sqrt {O{P^2} + O{N^2}} = \sqrt {{3^2} + {6^2}} = \sqrt {45} = 3\sqrt 5 {\rm{\;}}\left( {{\rm{cm}}} \right).\)
Diện tích của \(\Delta MNP\) là: \({S_{\Delta MNP}} = \frac{1}{2}PO \cdot MN = \frac{1}{2} \cdot 3 \cdot 9 = \frac{{27}}{2}\,\,\left( {\;{\rm{c}}{{\rm{m}}^2}} \right).\)
Chu vi tam giác \(MNP\) là: \(9 + 3\sqrt 2 + 3\sqrt 5 {\rm{\;}}\left( {{\rm{cm}}} \right).\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập