Câu hỏi:
10/03/2025 120Trong hệ trục tọa độ \(Oxy\) cho hai điểm \(M\left( {4; - 3} \right),N\left( {4;1} \right)\) và đường thẳng \(d:x + 6y = 0\). Tìm bán kính (kết quả làm tròn đến hàng phần trăm) của đường tròn \(\left( C \right)\) đi qua \(M\) và \(N\) biết rằng các tiếp tuyến của \(\left( C \right)\) tại \(M\) và \(N\) cắt nhau tại điểm \(Q\) thuộc \(d\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Trả lời: 2,83
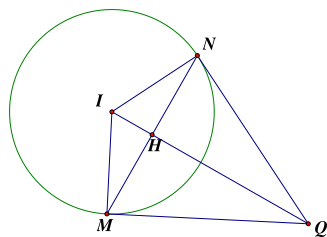
Gọi \(I\) là tâm của đường tròn \(\left( C \right)\), \(H\) là trung điểm của \(MN\).
Suy ra \(H\left( {4; - 1} \right)\), \(\overrightarrow {MN} = \left( {0;4} \right) = 4\left( {0;1} \right)\).
Đường thẳng \(IQ\) đi qua điểm \(H\left( {4; - 1} \right)\) và nhận \(\overrightarrow n \left( {0;1} \right)\) làm vectơ pháp tuyến có phương trình là:
\(y + 1 = 0\).
Tọa độ điểm \(Q\) là nghiệm của hệ \(\left\{ \begin{array}{l}x + 6y = 0\\y + 1 = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 6\\y = - 1\end{array} \right.\). Do đó \(Q\left( {6; - 1} \right)\).
Ta có \[\overrightarrow {MQ} = \left( {2;2} \right)\], \(\overrightarrow {NQ} = \left( {2; - 2} \right)\).
Đường thẳng \(IM\) đi qua \(M\left( {4; - 3} \right)\) và nhận \(\overrightarrow {MQ} \) làm vectơ pháp tuyến có phương trình là:
\(2\left( {x - 4} \right) + 2\left( {y + 3} \right) = 0\)\( \Leftrightarrow x + y - 1 = 0\).
Đường thẳng \(IN\) đi qua \(N\left( {4;1} \right)\) và nhận \(\overrightarrow {NQ} \) làm vectơ pháp tuyến có phương trình là:
\(2\left( {x - 4} \right) - 2\left( {y - 1} \right) = 0\)\( \Leftrightarrow x - y - 3 = 0\).
Tọa độ điểm \(I\) là nghiệm của hệ \(\left\{ \begin{array}{l}x + y = 1\\x - y = 3\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = - 1\end{array} \right.\). Do đó \(I\left( {2; - 1} \right)\).
Bán kính của đường tròn \(\left( C \right)\) là \(R = IM = \sqrt {{{\left( {4 - 2} \right)}^2} + {{\left( { - 3 + 1} \right)}^2}} = 2\sqrt 2 \approx 2,83\).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Điều kiện: \(n \ge 2,n \in \mathbb{N}\).
Ta có \(C_n^1 + C_n^2 = 15\)\( \Leftrightarrow n + \frac{{n\left( {n - 1} \right)}}{2} = 15\)\( \Leftrightarrow {n^2} + n - 30 = 0\)\( \Leftrightarrow \left[ \begin{array}{l}n = 5\\n = - 6\end{array} \right.\)\( \Rightarrow n = 5\).
Với \(n = 5\) ta có \({\left( {x + \frac{2}{{{x^4}}}} \right)^5} = {x^5} + 5.{x^4}.\frac{2}{{{x^4}}} + 10.{x^3}.{\left( {\frac{2}{{{x^4}}}} \right)^2} + 10.{x^2}.{\left( {\frac{2}{{{x^4}}}} \right)^3} + 5.x.{\left( {\frac{2}{{{x^4}}}} \right)^4} + {\left( {\frac{2}{{{x^4}}}} \right)^5}\)
\( = {x^5} + 10 + \frac{{40}}{{{x^5}}} + \frac{{80}}{{{x^{10}}}} + \frac{{80}}{{{x^{15}}}} + \frac{{32}}{{{x^{20}}}}\).
Số hạng không chứa \(x\) trong khai triển trên là \(10\).
Lời giải
Hướng dẫn giải
Sắp xếp mẫu số liệu trên theo thứ tự tăng dần ta được: 7; 8; 11; 13; 15; 18; 19; 20; 22.
Ta có \({Q_1} = \frac{{8 + 11}}{2} = 9,5\); \({Q_3} = \frac{{19 + 20}}{2} = 19,5\).
Suy ra \({\Delta _Q} = {Q_3} - {Q_1} = 19,5 - 9,5 = 10\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
13 câu Trắc nghiệm Tích của vectơ với một số có đáp án (Thông hiểu)
-
12 Bài tập Ứng dụng của hàm số bậc hai để giải bài toán thực tế (có lời giải)
-
16 câu Trắc nghiệm Toán 10 Kết nối tri thức Mệnh đề có đáp án
-
10 Bài tập Ứng dụng ba đường conic vào các bài toán thực tế (có lời giải)
-
Bộ 2 Đề kiểm tra giữa học kì 2 Toán 10 Kết nối tri thức có đáp án - Đề 1
-
10 Bài tập Tìm hệ số, số hạng trong khai triển nhị thức Newton (có lời giải)
-
10 Bài tập Cách xét tính đúng sai của mệnh đề (có lời giải)
-
15 câu Trắc nghiệm Toán 10 chân trời sáng tạo Không gian mẫu và biến cố có đáp án