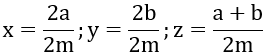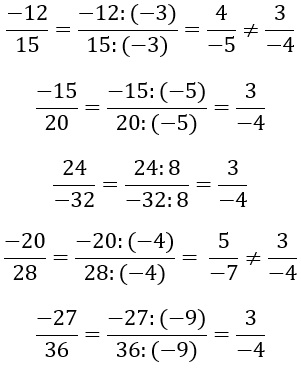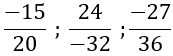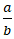Giả sử (a, b, m ∈ Z; m > 0) và x < y. Hãy chứng minh nếu chọn thì ta có x < z < y.
Hướng dẫn: Sử dụng tính chất: Nếu a, b, c ∈ Z và a < b thì a + c < b + c
Quảng cáo
Trả lời:
Theo đề bài ta có 
Quy đồng mẫu số các phân số ta được:
Nhận xét: mẫu số 2m > 0 nên để so sánh x, y, z ta so sánh các tử số 2a, 2b, a+b.
Vì a < b nên a + a < b + a hay 2a < a + b.
Vì a < b nên a + b < b + b hay a + b < 2b.
Vậy ta có 2a < a+b < 2b nên 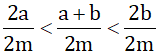
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 (chương trình mới) ( 126.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Biểu diễn trên trục số:
Ta viết:
Chia đoạn thẳng đơn vị thành 4 phần bằng nhau , ta được đơn vị mới bằng 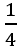
Số hữu tỉ 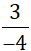
Lời giải
Ta có:
Vậy những phân số biểu diễn số hữu tỉ 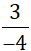
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.