B. TỰ LUẬN (3,0 điểm)
(1,0 điểm) Cô Hương đầu tư \(400\) triệu đồng vào hai khoản: mua trái phiếu doanh nghiệp với lãi suất \(8\% \) một năm và mua trái phiếu chính phủ với lãi suất \(6\% \) một năm. Cuối năm cô Hương nhận được \(29\) triệu đồng tiền lãi. Hỏi cô Hương đã đầu tư vào mỗi khoản bao nhiêu tiền?
B. TỰ LUẬN (3,0 điểm)
(1,0 điểm) Cô Hương đầu tư \(400\) triệu đồng vào hai khoản: mua trái phiếu doanh nghiệp với lãi suất \(8\% \) một năm và mua trái phiếu chính phủ với lãi suất \(6\% \) một năm. Cuối năm cô Hương nhận được \(29\) triệu đồng tiền lãi. Hỏi cô Hương đã đầu tư vào mỗi khoản bao nhiêu tiền?
Câu hỏi trong đề: Bộ 5 đề thi cuối kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi số tiền cô Hương dùng để mua trái phiếu doanh nghiệp là \(x\) (triều đồng) \(\left( {0 \le x \le 400} \right)\).
Khi đó, số tiền cô Hương dùng để mua trái phiếu chính phủ là \(400 - x\) (triệu đồng)
Số tiền lãi cô Hương nhận được từ trái phiếu doanh nghiệp là \(8\% .x\) hay \(0,08x\) (triệu đồng)
Số tiền lãi thu được từ trái phiếu chính phủ là \(0,06.\left( {400 - x} \right)\) (triệu đồng)
Theo đề, ta có phương trình \(0,08x + 0,06\left( {400 - x} \right) = 29\).
Giải phương trình, ta được: \(0,08x + 0,06\left( {400 - x} \right) = 29\)
\(0,08x + 24 - 0,06x = 29\)
\(0,02x + 24 = 29\)
\(0,02x = 5\)
\(x = 250\) (thỏa mãn)
Do đó, số tiền mua trái phiếu chính phủ của cô Hương là: \(400 - 250 = 150\) (triệu đồng)
Vậy cô Hương đã dùng \(250\) triệu đồng để mua trái phiếu doanh nghiệp, còn \(150\) triệu đồng để mua trái phiếu chính phủ.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án: \(24,6\)
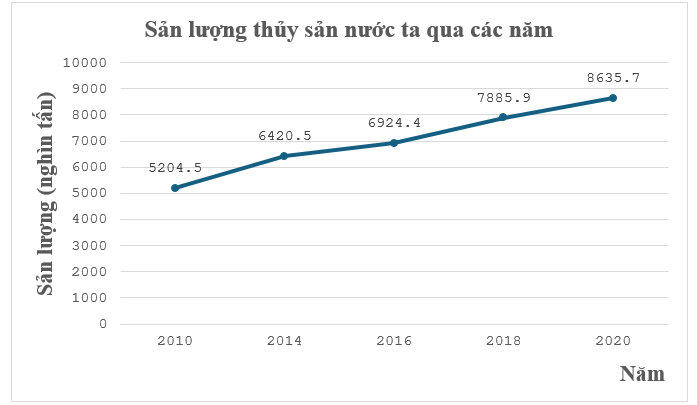
Tổng sản lượng thủy sản nước ta qua các năm là:
\(5{\rm{ }}204,5 + 6{\rm{ }}420,5 + 6{\rm{ }}924,4 + 7{\rm{ }}885,9 + 8{\rm{ }}635,7 = 35{\rm{ }}071\) (nghìn tấn)
Sản lượng thủy sản của nước ta năm 2020 so với tổng sản lượng thủy sản của nước ta qua các năm chiếm số phần trăm là: \(\frac{{8{\rm{ }}635,7}}{{35{\rm{ }}071}}.100\% \approx 24,6\% \).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
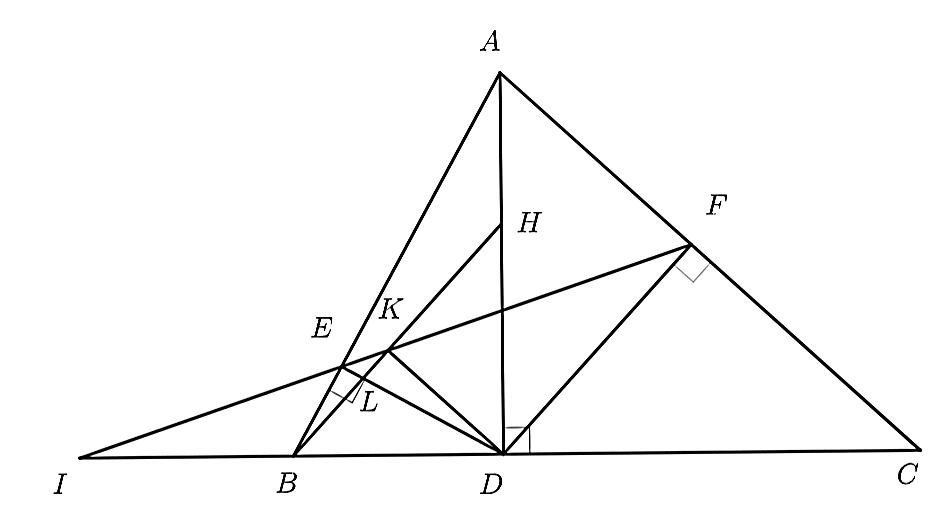
Xét \(\Delta AED\) và \(\Delta ADB\) có:
\(\widehat A\) chung
\(\widehat {AED} = \widehat {ADB} = 90^\circ \)
Suy ra (g.g)
Suy ra \(\frac{{AE}}{{AD}} = \frac{{AD}}{{AB}}\), suy ra \(AE.AB = A{D^2}\) (1)
Xét \(\Delta AFD\) và \(\Delta ADC\) có:
\(\widehat A\) chung
\(\widehat {AFD} = \widehat {ADC} = 90^\circ \) (gt)
Suy ra (g.g)
Suy ra \(\frac{{AF}}{{AD}} = \frac{{AD}}{{AC}}\) suy ra \(AF.AC = A{D^2}\) (2)
Từ (1) và (2) suy ra \(AE.AB = A{D^2} = AF.AC.\)
Do đó, \(\frac{{AE}}{{AF}} = \frac{{AC}}{{AB}}\).
Xét \(\Delta AEF\) và \(\Delta ACB\)có:
\(\widehat A\) chung
\(\frac{{AE}}{{AF}} = \frac{{AC}}{{AB}}\) (cmt)
Suy ra (c.g.c)
Suy ra \(\widehat {AEF} = \widehat {ACB}\).
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập