Trong không gian với hệ tọa độ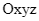 
, cho hai điểm 
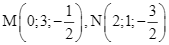và mặt phẳng 
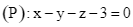. Gọi 
là đường thẳng thay đổi nằm trong mặt phẳng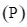 
, các điểm 
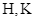lần lượt là hình chiếu vuông góc của 
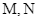trên . Biết rằng khi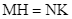 
thì trung điểm của 
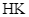luôn thuộc một đường thẳng 
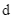cố định.
Phương trình tham số của đường thẳng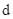 
là:
Trong không gian với hệ tọa độ , cho hai điểm và mặt phẳng . Gọi là đường thẳng thay đổi nằm trong mặt phẳng , các điểm lần lượt là hình chiếu vuông góc của trên . Biết rằng khi thì trung điểm của luôn thuộc một đường thẳng cố định.
là: A. 
.
.B. 
.
.C. 
.
.D. 
.
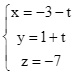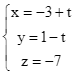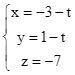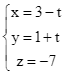.Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi 
lần lượt là trung điểm của 
và 
.
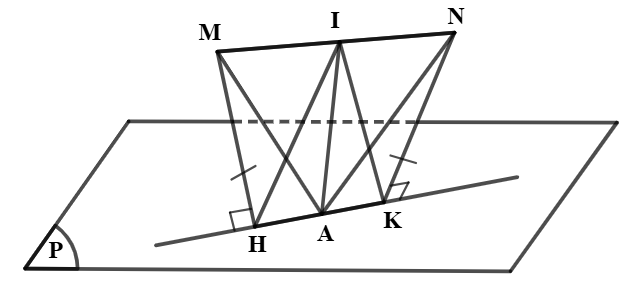
Ta có 
(c – g – c) 
Tam giác 
cân tại 
.
luôn thuộc mặt phẳng trung trực 
của đoạn thẳng .
là giao tuyến của hai mặt phẳng 
và .
Ta có 
. Phương trình mặt phẳng 
.
nên 
có một vectơ chỉ phương 
.
Lấy điểm 
, tọa độ của điểm 
thỏa mãn hệ 
.
Tìm được điểm 
.
Do đó phương trình tham số của đường thẳng là: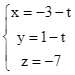 
. Chọn C.
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. Nàng Mị Châu ngây thơ, khờ khạo, cả tin nên bị lừa.
B. Nàng Mị Châu quá coi trọng tình cảm cá nhân đến nỗi mù quáng.
C. Nàng Mị Châu yêu Trọng Thuỷ đến nỗi cho Trọng Thuỷ xem nỏ thần.
D. Nàng Mị Châu hiền lành đến ngu ngốc.
Lời giải
Cần đặt câu thơ vào trong văn cảnh của đoạn thơ để giải thích: “Trái tim nhầm chỗ để trên đầu” nghĩa là đặt tình cảm riêng tư không đúng chỗ, suy xét mọi vấn đề chỉ dựa trên tình cảm, không xuất phát từ nhận thức, phân biệt đúng sai, dẫn đến thảm cảnh nước mất nhà tan. Trong các phương án trên, phương án B là gần với cách giải nghĩa nhất: suy xét mọi vấn đề chỉ dựa trên tình cảm nghĩa là “mù quáng”. Chọn B.
Lời giải
Gọi 
là không gian mẫu. Chọn 3 quả cầu từ 12 quả cầu, suy ra 
.
Gọi 
là biến cố: “Ba quả cầu được chọn có ba màu khác nhau”.
Chọn 1 quả cầu xanh: có 
cách.
Chọn 1 quả cầu đỏ: có 
cách.
Chọn 1 quả cầu vàng: có 
cách.
Khi đó, 
Vậy xác suất cần tính là 
. Chọn A.
Câu 3
A. Biến thiên entropy.
B. Biến thiên enthalpy.
C. Biến thiên năng lượng tự do Gibbs.
D. Năng lượng hoạt hóa.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Người kể chuyện hóa thân vào nhân vật chính để biết hết mọi chuyện.
B. Người kể chuyện mượn quan điểm, thái độ của một nhân vật nào đó.
C. Người kể chuyện có vai trò toàn năng với cái nhìn thông suốt tất cả, biết rõ hành động, suy nghĩ cảm giác của các nhân vật.
D. Người kể chuyện là quan sát viên.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. khởi nghĩa giành lại chính quyền.
B. dùng bạo lực cách mạng.
C. đấu tranh chính trị hòa bình.
D. đấu tranh vũ trang.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo