Câu hỏi:
05/04/2025 453
Câu 26 - 28: (1,5 điểm) Cho tam giác \(ABC\) vuông tại \(A\) có cạnh \(AB < AC\). Tia phân giác của góc \(\widehat {ABC}\) cắt \(AC\) ở \(D\). Trên cạnh \(BC\) lấy điểm \(E\) sao cho \(AB = BE\).
a) Chứng minh \(DE \bot BC\) và \(BD\) là đường trung trực của đoạn thẳng \(AE.\)
Câu 26 - 28: (1,5 điểm) Cho tam giác \(ABC\) vuông tại \(A\) có cạnh \(AB < AC\). Tia phân giác của góc \(\widehat {ABC}\) cắt \(AC\) ở \(D\). Trên cạnh \(BC\) lấy điểm \(E\) sao cho \(AB = BE\).
a) Chứng minh \(DE \bot BC\) và \(BD\) là đường trung trực của đoạn thẳng \(AE.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
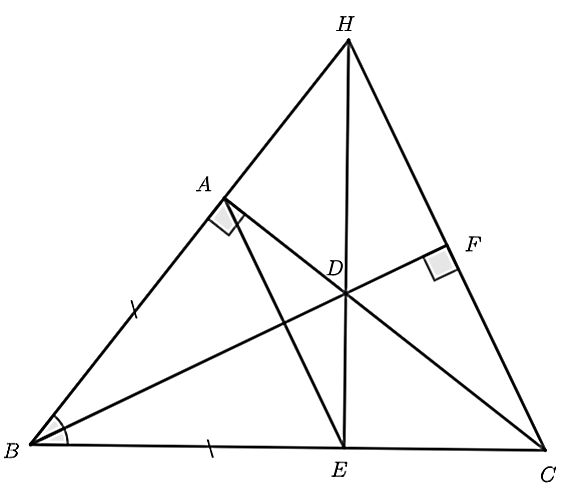
a) Xét \(\Delta ABD\) và \(\Delta EBD\), có:
\(AB = BE\) (gt)
\(\widehat {ABD} = \widehat {DBE}\) (gt)
\(BD\) chung (gt)
Do đó, \(\Delta ABD = \Delta EBD\) (c.g.c)
Suy ra \(\widehat {BAD} = \widehat {DEB} = 90^\circ \) (hai góc tương ứng)
Do đó, \(DE \bot BC\).
Ta có \(AB = BE\) (gt) nên \(B\) thuộc đường trung trực của \(AE\) và \(AD = DE\) (hai cạnh tương ứng) nên \(D\) thuộc đường trung trực của \(AE\).
Suy ra \(BD\) là đường trung trực của đoạn thẳng \(AE.\)
Câu hỏi cùng đoạn
Câu 2:
b) So sánh \(DA\) và \(DC.\)
b) So sánh \(DA\) và \(DC.\)
Lời giải của GV VietJack
b) Vì \(\Delta ABD = \Delta EBD\) (c.g.c) nên \(AD = DE\) (hai cạnh tương ứng) (1)
Xét tam giác \(EDC\) có \(\widehat {DEC} = 90^\circ \) nên \(DC > DE\) (2)
Từ (1) và (2) suy ra \(AD < DC.\)
Câu 3:
c) Hạ \(CF\) vuông góc với tia \(BD\) tại \(F\). Chứng minh ba đường thẳng \(AB,DE,CF\) đồng quy.
c) Hạ \(CF\) vuông góc với tia \(BD\) tại \(F\). Chứng minh ba đường thẳng \(AB,DE,CF\) đồng quy.
Lời giải của GV VietJack
c) Xét tam giác \(BDC\) có \(CF \bot BD\) tại \(F\), \(ED \bot BC\) tại \(E\) và \(BA \bot DC\) tại \(A\).
Mà \(CF,BA,DE\) là ba đường cao trong tam giác \(BDC\).
Do đó, \(AB,DE,CF\) đồng quy tại trực tâm \(H\) (nằm ngoài tam giác \(BDC\)).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Số các số có hai chữ số là: \(\left( {99 - 10} \right):1 + 1 = 90\) (số).
Xét từ \(10\) đến \(20\) có các số chia hết cho 2 mà không chia hết cho 5 là: \(12;14;16;18.\) Do đó, có 4 số.
Tương tự, ta xét được từ \(20\) đến 30; 30 đến 40;…..80 đến 90.
Do đó, từ \(10\) đến \(90\) có \(4.9 = 36\) số chia hết cho 2 nhưng không chia hết cho 5.
Vậy xác suất để Lan bốc trúng số có hai chữ số chia hết cho 2 mà không chia hết cho 5 là \(\frac{{36}}{{90}} = \frac{2}{5}.\)
Lời giải
Đáp án: \(3450\)
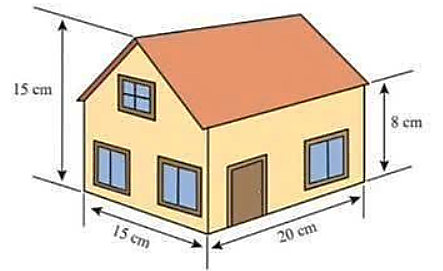
Ta có hình vẽ hình học mô phỏng ngôi nhà dưới đây.
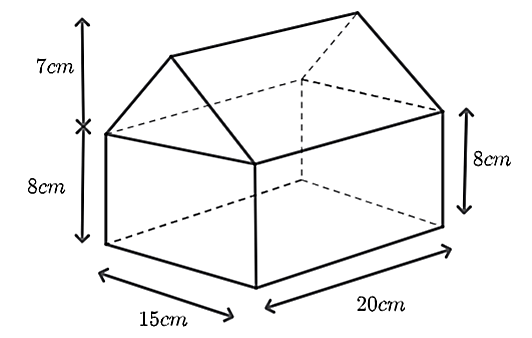
Nhận thấy, thể tích ngôi nhà gồm thể tích hình lăng trụ đứng tam giác (phần mái) và thể tích hình hộp chữ nhật (phần nhà).
Ta có thể tích hình lăng trụ đứng tam giác là \({V_1} = S.h = \frac{1}{2}.7.15.20 = 1{\rm{ }}050{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Thể tích hình hộp chữ nhật là \({V_1} = abc = 8.15.20 = 2{\rm{ }}400{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Vậy thể tích của ngôi nhà là: \({V_1} + {V_2} = 1{\rm{ }}050 + 2{\rm{ }}400 = 3{\rm{ }}450{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
-
15 câu Trắc nghiệm Toán 7 Cánh diều Bài 1: Tập hợp Q các số hữu tỉ có đáp án
-
15 câu Trắc nghiệm Toán 7 Chân trời sáng tạo Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
-
Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất) - đề 2