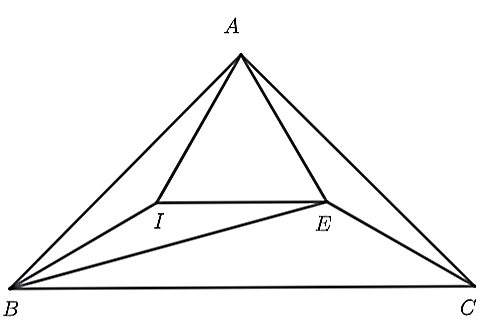
Cho \(\Delta ABC,\) \(\widehat B = \widehat C = 45^\circ \). Điểm \(E\) nằm trong tam giác sao cho \(\widehat {EAC} = \widehat {ECA} = 15^\circ \). Tính \(\widehat {BEA}\)?
Cho \(\Delta ABC,\) \(\widehat B = \widehat C = 45^\circ \). Điểm \(E\) nằm trong tam giác sao cho \(\widehat {EAC} = \widehat {ECA} = 15^\circ \). Tính \(\widehat {BEA}\)?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án: \(75\)
|
Vẽ \(\Delta AEI\) đều (\(I,B\) cùng phía so với \(AE\)). Vì \(\Delta ABC\) có \(\widehat B = \widehat C = 45^\circ \) nên \(\Delta ABC\) cân tại \(A\). Ta có: \(\widehat A = 180^\circ - \left( {\widehat B + \widehat C} \right) = 90^\circ \). Do đó, ta có: \(\widehat {BAI} + \widehat {IAE} + \widehat {EAC} = 90^\circ \) nên \(\widehat {BAI} = 15^\circ \). Suy ra \(\widehat {BAI} = \widehat {CAE} = 15^\circ \). Xét \(\Delta AEC\) và \(\Delta AIB\), có: \(AI = AE\) (gt) \(AB = AC\) (\(\Delta ABC\) cân tại \(A\)). \(\widehat {BAI} = \widehat {CAE} = 15^\circ \) (cmt) Ta có: \(\Delta AEC = \Delta AIB\) (c.g.c) Suy ra \(IB = CE\) mà \(EI = CE\) (\(\Delta AEI\) đều) Do đó, \(IB = EI\) suy ra \(\Delta EIB\) cân tại \(I\). Suy ra \(\widehat {EIB} = 360^\circ - \left( {60^\circ + 150^\circ } \right) = 150^\circ \). Do đó, \(\widehat {IEB} = 15^\circ \). Suy ra \(\widehat {BEA} = \widehat {BEI} + \widehat {IEA} = 75^\circ \) |
|
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. “Mặt xuất hiện có số chấn nhỏ hơn 7”.
B. “Mặt xuất hiện có số chấm chia hết cho 7”.
C. “Mặt xuất hiện có số chấm lớn hơn 4”.
D. “Mặt xuất hiện có số chấm nhỏ hơn 2”.
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Do các số chấm xuất hiện trên con xúc xắc là: \(1;2;3;4;5;6\) nên biến cố “Mặt xuất hiện có số chấm nhỏ hơn 7” là biến cố chắc chắn.
Lời giải
Hướng dẫn giải
Đáp án: \(3\)
Thực hiện chia đa thức \(h\left( x \right) = {x^3} + 3{x^2} + 5x + m\) cho \(x + 1\), ta được:
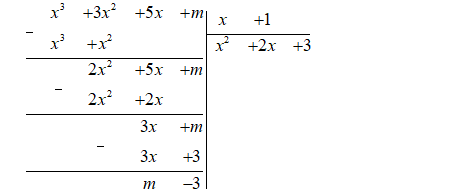
Do đó, có \(\left( {{x^3} + 3{x^2} + 5x + m} \right):\left( {x + 1} \right) = {x^2} + 2x + 3\) và dư \(m - 3\).
Để đa thức \(h\left( x \right)\) chia hết cho \(x + 1\) thì \(m - 3 = 0\) hay \(m = 3\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Cho \(\Delta ABC\) có \(I\) là giao điểm của ba đường phân giác trong \(\Delta ABC\). Khi đó, ta có:
A. \(AI\) vuông góc với \(BC.\)
B. \(I\) cách đều ba đỉnh của \(\Delta ABC\).
C. \(\Delta ABI\) cân ở \(I.\)
D. \(I\) cách đều ba cạnh của \(\Delta ABC\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(40x.\)
B. \(40 + x.\)
C. \(40:x.\)
D. \(\frac{x}{{40}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo