B. TỰ LUẬN (3,0 điểm)
Câu 25-27. (1,5 điểm) Cho hai đa thức \(A\left( x \right) = 2{x^3} - 3{x^2} + 4x + 3\) và \(B\left( x \right) = 2{x^2} + 3{x^3} - 6\).
a) Tính \(A\left( x \right) + B\left( x \right)\) và \(A\left( x \right) - B\left( x \right)\).
B. TỰ LUẬN (3,0 điểm)
Câu 25-27. (1,5 điểm) Cho hai đa thức \(A\left( x \right) = 2{x^3} - 3{x^2} + 4x + 3\) và \(B\left( x \right) = 2{x^2} + 3{x^3} - 6\).
a) Tính \(A\left( x \right) + B\left( x \right)\) và \(A\left( x \right) - B\left( x \right)\).
Quảng cáo
Trả lời:
a) Ta có: \(A\left( x \right) + B\left( x \right) = 2{x^3} - 3{x^2} + 4x + 3 + 2{x^2} + 3{x^3} - 6\)
\( = \left( {2{x^3} + 3{x^3}} \right) + \left( {2{x^2} - 3{x^2}} \right) + 4x + 3 - 6\)
\( = 5{x^2} - {x^2} + 4x - 3\).
\(A\left( x \right) - B\left( x \right) = 2{x^3} - 3{x^2} + 4x + 3 - \left( {2{x^2} + 3{x^3} - 6} \right)\)
\( = 2{x^3} - 3{x^2} + 4x + 3 - 2{x^2} - 3{x^3} + 6\)
\( = \left( {2{x^3} - 3{x^3}} \right) + \left( { - 2{x^2} - 3{x^2}} \right) + 4x + 3 + 6\)
\( = - {x^3} - 5{x^2} + 4x + 9\).
Câu hỏi cùng đoạn
Câu 2:
b) Tìm đa thức \(C\left( x \right)\) biết \(\left( {2x + 1} \right).C\left( x \right) = A\left( x \right)\).
b) Tìm đa thức \(C\left( x \right)\) biết \(\left( {2x + 1} \right).C\left( x \right) = A\left( x \right)\).
b) Ta có: \(\left( {2x + 1} \right).C\left( x \right) = A\left( x \right)\) nên \(C\left( x \right) = A\left( x \right):\left( {2x + 1} \right)\).
Suy ra \(C\left( x \right) = \left( {2{x^3} - 3{x^2} + 4x + 3} \right):\left( {2x + 1} \right) = {x^2} - 2x + 3\).
Vậy \(C\left( x \right) = {x^2} - 2x + 3\).
Câu 3:
c) Chứng minh rằng \(3A\left( x \right) - 2B\left( x \right) + 13{x^2} - 12x\) có giá trị không phụ thuộc vào \(x.\)
c) Chứng minh rằng \(3A\left( x \right) - 2B\left( x \right) + 13{x^2} - 12x\) có giá trị không phụ thuộc vào \(x.\)
c) Ta có: \(3A\left( x \right) - 2B\left( x \right) + 13{x^2} - 12x = 3\left( {2{x^3} - 3{x^2} + 4x + 3} \right) - 2\left( {2{x^2} + 3{x^3} - 6} \right) + 13{x^2} - 12x\)
\( = 6{x^3} - 9{x^2} + 12x + 9 - 4{x^2} - 6{x^3} + 12 + 13{x^2} - 12x\)
\( = \left( {6{x^3} - 6{x^3}} \right) + \left( { - 9{x^2} - 4{x^2} + 13{x^2}} \right) + \left( {12x - 12x} \right) + 21\)
\( = 21.\)
Vậy \(3A\left( x \right) - 2B\left( x \right) + 13{x^2} - 12x = 21\) nên có giá trị không phụ thuộc vào \(x\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 (chương trình mới) ( 126.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Do các số chấm xuất hiện trên con xúc xắc là: \(1;2;3;4;5;6\) nên biến cố “Mặt xuất hiện có số chấm nhỏ hơn 7” là biến cố chắc chắn.
Lời giải
Hướng dẫn giải
Đáp án: \(3\)
Thực hiện chia đa thức \(h\left( x \right) = {x^3} + 3{x^2} + 5x + m\) cho \(x + 1\), ta được:
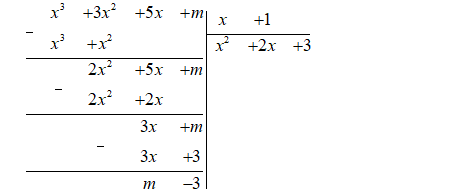
Do đó, có \(\left( {{x^3} + 3{x^2} + 5x + m} \right):\left( {x + 1} \right) = {x^2} + 2x + 3\) và dư \(m - 3\).
Để đa thức \(h\left( x \right)\) chia hết cho \(x + 1\) thì \(m - 3 = 0\) hay \(m = 3\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Cho \(\Delta ABC\) có \(I\) là giao điểm của ba đường phân giác trong \(\Delta ABC\). Khi đó, ta có:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.