Câu 28-30. (1,5 điểm) Cho tam giác \(ABC\) cân tại \(A\), vẽ \(AH\) vuông góc với \(BC\) tại \(H.\)
a) Chứng minh \(\Delta AHB = \Delta AHC.\)
Câu 28-30. (1,5 điểm) Cho tam giác \(ABC\) cân tại \(A\), vẽ \(AH\) vuông góc với \(BC\) tại \(H.\)
a) Chứng minh \(\Delta AHB = \Delta AHC.\)
Quảng cáo
Trả lời:
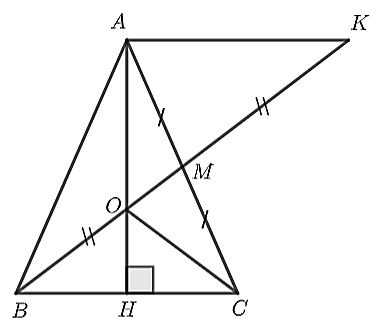
a) Xét \(\Delta AHB\) và \(\Delta AHC\) có:
\(\widehat {AHB} = \widehat {AHC} = 90^\circ \) (Vì \(AH\) vuông góc với \(BC\) tại \(H\))
\(AB = AC\) (\(\Delta ABC\) cân tại \(A\))
\(AH\) là cạnh chung
Suy ra \(\Delta AHB = \Delta AHC\) (ch – cgv)
Câu hỏi cùng đoạn
Câu 2:
b) Vẽ trung tuyến \(BM\) của \(\Delta ABC\). Trên tia đối của tia \(MB\) lấy điểm \(K\) sao cho \(MK = MB.\) Chứng minh \(\widehat {KAM} = \widehat {ABC}\).
b) Vẽ trung tuyến \(BM\) của \(\Delta ABC\). Trên tia đối của tia \(MB\) lấy điểm \(K\) sao cho \(MK = MB.\) Chứng minh \(\widehat {KAM} = \widehat {ABC}\).
b) Xét \(\Delta BMC\) và \(\Delta KMA\), ta có:
\(\widehat {BMC} = \widehat {KMA}\) (đối đỉnh)
\(MA = MC\) (\(BM\) là trung tuyến của \(\Delta ABC\))
\(MB = MK\) (gt)
Suy ra \(\Delta BMC = \Delta KMA\) (c.g.c)
Do đó, \(\widehat {KAM} = \widehat {BCM}\) (hai góc tương ứng)
Mà \(\widehat {ABC} = \widehat {BCM}\) (vì \(\Delta ABC\) cân tại \(A\)) nên \(\widehat {KAM} = \widehat {ABC}\).
Câu 3:
c) Gọi \(O\) là giao điểm của \(AH\) và \(BM.\) Chứng minh rằng \(OK = 2OC.\)
c) Gọi \(O\) là giao điểm của \(AH\) và \(BM.\) Chứng minh rằng \(OK = 2OC.\)
c) Theo câu a) ta có \(\Delta AHB = \Delta AHC\) nên \(BH = CH\) (hai cạnh tương ứng)
Nên \(AH\) là đường trung tuyến của \(\Delta ABC\).
Xét \(\Delta ABC\) có hai đường trung tuyến \(AH,BM\) cắt nhau tại \(O.\)
Nên \(O\) là trọng tâm của \(\Delta ABC\).
Suy ra \(OM = \frac{1}{3}BM\) và \(OB = \frac{2}{3}BM\) (1).
Xét \(\Delta OHB\) và \(\Delta OHC\), ta có:
\(\widehat {OHB} = \widehat {OHC} = 90^\circ \)
\(HB = HC\) (cmt)
\(OH\) chung
Suy ra \(\Delta OHB = \Delta OHC\) (c.g.c)
Nên \(OB = OC\) (hai cạnh tương ứng) (2)
Ta có: \(OK = OM + MK\)
Suy ra \(OK = \frac{1}{3}BM + BM\) (vì \(MK = BM\) và \(OM = \frac{1}{3}BM\))
Vậy \(OK = \frac{4}{3}BM\) (3)
Từ (1) và (2) suy ra \(OC = \frac{2}{3}BM\) (4)
Từ (3) và (4) suy ra \(OK = 2.\frac{2}{3}BM = 2OC.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 (chương trình mới) ( 126.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Do các số chấm xuất hiện trên con xúc xắc là: \(1;2;3;4;5;6\) nên biến cố “Mặt xuất hiện có số chấm nhỏ hơn 7” là biến cố chắc chắn.
Lời giải
Hướng dẫn giải
Đáp án: \(3\)
Thực hiện chia đa thức \(h\left( x \right) = {x^3} + 3{x^2} + 5x + m\) cho \(x + 1\), ta được:
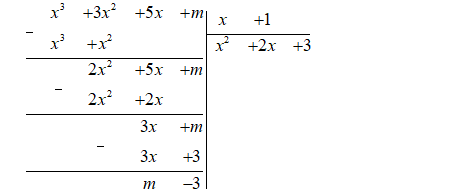
Do đó, có \(\left( {{x^3} + 3{x^2} + 5x + m} \right):\left( {x + 1} \right) = {x^2} + 2x + 3\) và dư \(m - 3\).
Để đa thức \(h\left( x \right)\) chia hết cho \(x + 1\) thì \(m - 3 = 0\) hay \(m = 3\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Cho \(\Delta ABC\) có \(I\) là giao điểm của ba đường phân giác trong \(\Delta ABC\). Khi đó, ta có:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.