Câu 28-30. (1,5 điểm) Cho tam giác \(ABC\) cân tại \(B,\widehat {ABC} = 80^\circ \). Lấy điểm \(I\) ở bên trong tam giác sao cho \(\widehat {IAC} = 10^\circ ,\widehat {ICA} = 30^\circ .\) Đường phân giác của \(\widehat {BAI}\) cắt đường thẳng \(CI\) tại \(K\)
a) Chứng minh tam giác \(ACK\) cân tại \(K.\)
Câu 28-30. (1,5 điểm) Cho tam giác \(ABC\) cân tại \(B,\widehat {ABC} = 80^\circ \). Lấy điểm \(I\) ở bên trong tam giác sao cho \(\widehat {IAC} = 10^\circ ,\widehat {ICA} = 30^\circ .\) Đường phân giác của \(\widehat {BAI}\) cắt đường thẳng \(CI\) tại \(K\)
a) Chứng minh tam giác \(ACK\) cân tại \(K.\)
Quảng cáo
Trả lời:
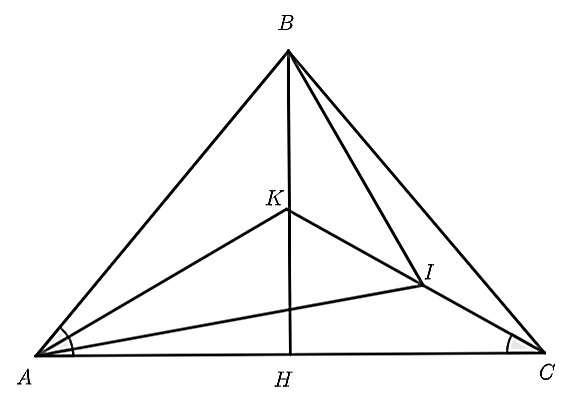
a) Vì tam giác \(ABC\) cân tại \(B,\) có \(\widehat {ABC} = 80^\circ \) nên \(\widehat {BAC} = \widehat {ACB} = \frac{{180^\circ - 80^\circ }}{2} = 50^\circ \).
Ta có \(\widehat {IAC} = 10^\circ \) nên \(\widehat {IAB} = \widehat {CAB} - \widehat {IAC} = 50^\circ - 10^\circ = 40^\circ \).
Mà \(AK\) là đường phân giác của \(\widehat {IAB}\) nên \(\widehat {BAK} = \widehat {KAI} = 20^\circ \).
Do đó, \(\widehat {KAC} = \widehat {KAI} + \widehat {IAC} = 20^\circ + 10^\circ = 30^\circ = \widehat {KCA}\)
Suy ra \(\widehat {CAK} = \widehat {KAC} = 30^\circ \) nên \(\Delta ACK\) cân tại \(K.\)
Câu hỏi cùng đoạn
Câu 2:
b) Chứng minh \(\Delta ABK = \Delta CBK\). Suy ra \(BK\) là phân giác của góc \(ABC\).
b) Chứng minh \(\Delta ABK = \Delta CBK\). Suy ra \(BK\) là phân giác của góc \(ABC\).
b) Có \(\Delta ACK\) cân tại \(K\) nên \(KA = KC.\)
Xét \(\Delta ABK\) và \(\Delta CBK\) có: \(AB = BC\) (gt), \(BK\) chung, \(KA = KC\).
Do đó, \(\Delta ABK = \Delta CBK\) (c.c.c).
Suy ra \(\widehat {ABK} = \widehat {CBK}\) (hai góc tương ứng).
Do đó, \(BK\) là phân giác của góc \(ABC\).
Câu 3:
c) Tính số đo \(\widehat {AIB}\).
c) Tính số đo \(\widehat {AIB}\).
c) Từ b) \(\Delta ABK = \Delta CBK\) (c.c.c) nên \(\widehat {AKB} = \widehat {CKB}\) (hai góc tương ứng)
Có \(BK\) là phân giác của góc \(ABC\) nên \(\widehat {ABK} = \widehat {CBK} = \frac{{\widehat {ABC}}}{2} = 40^\circ \).
Do đó, \(\widehat {AKB} = \widehat {CKB} = 180^\circ - \left( {\widehat {KAB} + \widehat {KBA}} \right) = 180^\circ - \left( {40^\circ + 20^\circ } \right) = 120^\circ \).
Lại có \(\widehat {AKB} + \widehat {CKB} + \widehat {AKC} = 360^\circ \) nên \(\widehat {CKA} = 360^\circ - 2.120^\circ = 120^\circ \).
Do đó, \(\widehat {AKB} = \widehat {CKB} = \widehat {CKA}\).
Xét \(\Delta AKB\) và \(\Delta AKI\), có: \(\widehat {KAB} = \widehat {KAI}\) (gt); \(AK\) chung (gt); \(\widehat {AKB} = \widehat {CKA}\) (cmt)
Do đó, \(\Delta AKB = \Delta AKI\) (g.c.g)
Suy ra \(AB = AI\) (hai cạnh tương ứng)
Do đó, \(\Delta AIB\) cân tại \(A\) nên \(\widehat {ABI} = \widehat {AIB} = \frac{{180^\circ - \widehat {BAI}}}{2} = \frac{{180^\circ - 40^\circ }}{2} = 70^\circ \).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 (chương trình mới) ( 126.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đ
a) Khi gieo một con xúc xắc 6 mặt cân đối, các kết quả có thể xảy ra là: xuất hiện mặt 1 chấm, mặt 2 chấm, mặt 3 chấm, mặt 4 chấm, mặt 5 chấm, mặt 6 chấm.
Các mặt xúc xắc có số chấm nhỏ hơn 8 nên biến cố “Mặt xuất hiện có số chấm nhỏ hơn 8” là biến cố chắc chắn.
Lời giải
S
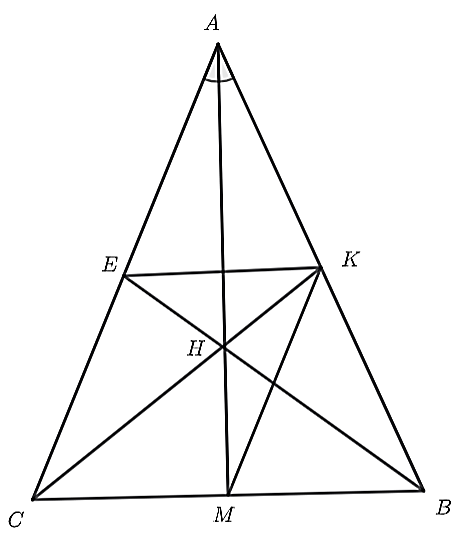
a) Xét \(\Delta ABM\) và \(\Delta AMC\) có:
\(AM\) chung (gt)
\(\widehat {CAM} = \widehat {MAB}\) (gt)
\(AB = AC\) (gt)
Do đó, \(\Delta ABM = \Delta ACM\) (c.g.c).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.