Câu 9-11. (2,5 điểm) Cho tam giác \[ABC\] vuông tại \[A\,\,\,\left( {AB < AC} \right),\] vẽ đường cao \[AH.\]
a) Chứng minh:
Câu 9-11. (2,5 điểm) Cho tam giác \[ABC\] vuông tại \[A\,\,\,\left( {AB < AC} \right),\] vẽ đường cao \[AH.\]
a) Chứng minh:
Quảng cáo
Trả lời:
Giải bởi Vietjack
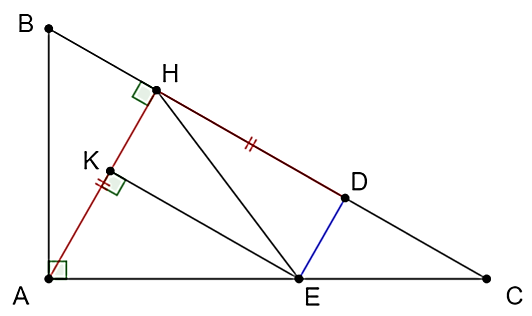
a) Xét \[\Delta ABH\] và \[\Delta CAB\] có:
\[\widehat {ABH} = \widehat {CBA}\;\,\left( {\widehat B\;\,{\rm{chung}}} \right)\]
\(\widehat {AHB} = \widehat {CAB}\;\left( { = 90^\circ } \right)\)
Do đóCâu hỏi cùng đoạn
Câu 2:
b) Chứng minh: \(A{H^2} = HB \cdot HC\).
b) Chứng minh: \(A{H^2} = HB \cdot HC\).
Giải bởi Vietjack
b) Xét hai tam giác vuông \[ABC\] và \[ABH\] có:
\(\widehat {ABC} + \widehat {ACB} = 180^\circ - \widehat {BAC} = 90^\circ \)
\(\widehat {ABH} + \widehat {BAH} = 180^\circ - \widehat {AHB} = 90^\circ \)
Do đó \(\widehat {ACB} = \widehat {BAH}\) (vì cùng phụ với \(\widehat {ABC}\))
Xét \[\Delta ABH\] và \[\Delta CAH\] có:
\(\widehat {BAH} = \widehat {ACH}\;\,\left( {{\rm{cmt}}} \right)\); \(\widehat {AHB} = \widehat {CHA}\;\,\left( { = 90^\circ } \right)\)
Do đó .
Suy ra \(\frac{{AH}}{{CH}} = \frac{{BH}}{{AH}}\) hay \(A{H^2} = HB \cdot HC\) (đpcm).
Câu 3:
c) Trên tia \[HC,\] lấy điểm \(D\) sao cho \[HD = HA.\] Từ \(D\) vẽ đường thẳng song song \[AH\] cắt \[AC\] tại \[E.\] Chứng minh \[AE = AB.\]
c) Trên tia \[HC,\] lấy điểm \(D\) sao cho \[HD = HA.\] Từ \(D\) vẽ đường thẳng song song \[AH\] cắt \[AC\] tại \[E.\] Chứng minh \[AE = AB.\]
Giải bởi Vietjack
c) Ta có \[AH \bot BC\] mà \[DE{\rm{ // }}AH\] nên suy ra \[DE \bot BC\].
Gọi \[K\] là hình chiếu của \[E\] lên \[AH\].
Từ đó suy ra tứ giác \[EDHK\] là hình chữ nhật có:
• \(\widehat {EKH} = 90^\circ \) nên \(\widehat {AKE} = 90^\circ \).
• \[EK = HD = HA\].
Lại có:
• \(\widehat {BAC} = \widehat {BAH} + \widehat {KAE} = 90^\circ \).
• \(\widehat {KAE} + \widehat {KEA} = 180^\circ - \widehat {AKE} = 90^\circ \).
Nên suy ra \(\widehat {AEK} = \widehat {BAH}\) (vì cùng phụ với \(\widehat {KAE}\)).
Xét \[\Delta AKE\] và \[\Delta BHA\] có:
\(\widehat {AKE} = \widehat {BHA}\;\,\left( { = 90^\circ } \right)\); \(EK = AH\;\left( {{\rm{cmt}}} \right)\); \(\widehat {AEK} = \widehat {BAH}\;\left( {{\rm{cmt}}} \right)\)
Do đó \(\Delta AKE = \Delta BHA\;\,\left( {{\rm{g}}{\rm{.c}}{\rm{.g}}} \right)\).
Từ đó suy ra \[AE = AB\] (hai cạnh tương ứng).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chiếc bút thứ nhất chọn \[1\] trong số \[15\] chiếc bút nên có \[15\] cách.
Chiếc bút thứ hai chọn \[1\] trong \[14\] chiếc bút còn lại nên có \[14\] cách.
Số cách chọn \[2\] chiếc bút là \[\frac{{15 \cdot 14}}{2} = 105\] (cách) (cứ mỗi cặp bị lăp lại 2 lần).
Chiếc bút chì chọn \[1\] trong \[3\] chiếc nên có 3 cách.
Chiếc thứ hai chọn \[1\] trong \[12\] chiếc bút mực nên có \[12\] cách.
Số cách chọn ra \(2\) chiếc bút trong đó có \(1\) chiếc bút chì và một chiếc bút mực là \[3 \cdot 12 = 36\] (cách).
Xác suất của biến cố: “Bạn Tú lấy được \(1\) chiếc bút chì và \(1\) chiếc bút mực” là \(\frac{{36}}{{105}} = \frac{{12}}{{35}}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
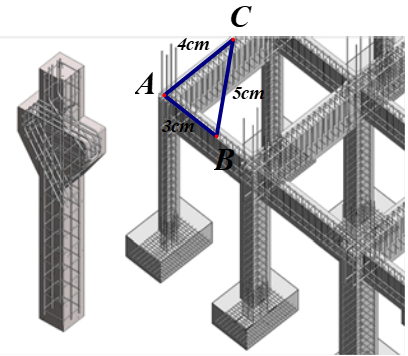
Xét tam giác \[ABC\] ta có:
\(B{C^2} = {5^2} = 25;\) \(A{B^2} + A{C^2} = {3^2} + {4^2} = 25\)
Do đó \(B{C^2} = A{B^2} + A{C^2}.\)
Theo định lý Pythagore đảo thì tam giác \[ABC\] vuông tại \[A.\]
Vậy hai phần móng đó vuông góc với nhau.Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập