Câu hỏi:
21/04/2025 543
Câu 12-13.(1,5 điểm)
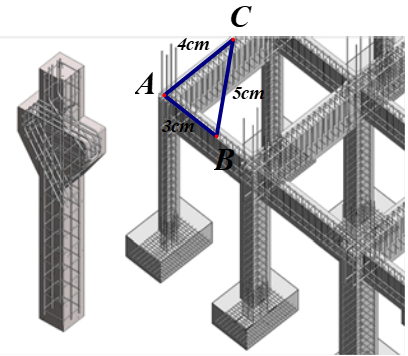
Khi xây móng nhà, để kiểm tra xem hai phần móng có vuông góc với nhau hay không, người thợ xây thường lấy \[AB = 3\,\,{\rm{cm}},{\rm{ }}AC = 4\,\,{\rm{cm}}\] \[(A\] là điểm chung của hai phần móng nhà hay còn gọi là góc nhà), rồi đo đoạn \[BC\] nếu \[BC = 5\,\,{\rm{cm}}\] thì hai phần móng đó vuông góc với nhau. Hãy giải thích vì sao?
Câu 12-13.(1,5 điểm)
Khi xây móng nhà, để kiểm tra xem hai phần móng có vuông góc với nhau hay không, người thợ xây thường lấy \[AB = 3\,\,{\rm{cm}},{\rm{ }}AC = 4\,\,{\rm{cm}}\] \[(A\] là điểm chung của hai phần móng nhà hay còn gọi là góc nhà), rồi đo đoạn \[BC\] nếu \[BC = 5\,\,{\rm{cm}}\] thì hai phần móng đó vuông góc với nhau. Hãy giải thích vì sao?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Xét tam giác \[ABC\] ta có:
\(B{C^2} = {5^2} = 25;\) \(A{B^2} + A{C^2} = {3^2} + {4^2} = 25\)
Do đó \(B{C^2} = A{B^2} + A{C^2}.\)
Theo định lý Pythagore đảo thì tam giác \[ABC\] vuông tại \[A.\]
Vậy hai phần móng đó vuông góc với nhau.Câu hỏi cùng đoạn
Câu 2:
Một chậu cây cảnh mini có hình dạng là một hình chóp tứ giác đều có chiều cao bằng \(35\,\,{\rm{cm}}\), cạnh đáy bằng \(24\,\,{\rm{cm}}\). Tính độ dài trung đoạn của chậu cây cảnh.
Lời giải của GV VietJack
Ta có \(SE\) là trung đoạn nên \(E\) là trung điểm của \(AB\).
Xét \(\Delta ABD\) có \(E,\,\,H\) lần lượt là trung điểm của \(AB,\,\,BD\).
Do đó \(EH\) là đường trung bình của \(\Delta ABD\) nên \(EH = \frac{1}{2}AD = 12\,\,\left( {{\rm{cm}}} \right)\).
Xét \(\Delta SEH\) vuông tại \(H\) có: \(S{E^2} = S{H^2} + E{H^2}\)
\(S{E^2} = {35^2} + {12^2}\)
\(SE = 37\,\,{\rm{cm}}\).
Vậy độ dài trung đoạn của chậu cây cảnh là 37 cm.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chiếc bút thứ nhất chọn \[1\] trong số \[15\] chiếc bút nên có \[15\] cách.
Chiếc bút thứ hai chọn \[1\] trong \[14\] chiếc bút còn lại nên có \[14\] cách.
Số cách chọn \[2\] chiếc bút là \[\frac{{15 \cdot 14}}{2} = 105\] (cách) (cứ mỗi cặp bị lăp lại 2 lần).
Chiếc bút chì chọn \[1\] trong \[3\] chiếc nên có 3 cách.
Chiếc thứ hai chọn \[1\] trong \[12\] chiếc bút mực nên có \[12\] cách.
Số cách chọn ra \(2\) chiếc bút trong đó có \(1\) chiếc bút chì và một chiếc bút mực là \[3 \cdot 12 = 36\] (cách).
Xác suất của biến cố: “Bạn Tú lấy được \(1\) chiếc bút chì và \(1\) chiếc bút mực” là \(\frac{{36}}{{105}} = \frac{{12}}{{35}}\).
Lời giải
Trong 50 lần thử, số lần gieo được mặt có số chấm là số chẵn là:
\[9 + 5 + 13 = 27\] (lần).
Vậy số lần gieo được mặt có số chấm là số chẵn là 27.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Dạng 1: Bài luyện tập 1 dạng 1: Tính có đáp án
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 24
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Đề cuối kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 1
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 2)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận