Dựa vào thông tin dưới đây để trả lời các câu từ 77 đến 78
Cho phương trình \({4^x} - m \cdot {2^{x + 1}} + m + 2 = 0\) với \(m\) là tham số thực.
Giả sử phương trình có 2 nghiệm \({x_1},{x_2}\). Khi đó \({x_1} + {x_2}\) bằng
Dựa vào thông tin dưới đây để trả lời các câu từ 77 đến 78
Cho phương trình \({4^x} - m \cdot {2^{x + 1}} + m + 2 = 0\) với \(m\) là tham số thực.
Câu hỏi trong đề: Đề thi ĐGNL ĐHQG Hồ Chí Minh (V-ACT) năm 2026-2027 (Đề 18) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đặt \(t = {2^x}\), phương trình đã cho trở thành: \({t^2} - 2mt + m + 2 = 0\,\,\left( 1 \right)\).
Giả sử phương trình có 2 nghiệm \({t_1},{t_2}\). Khi đó theo Vi-et ta có \({t_1}{t_2} = m + 2\).
Suy ra \({2^{{x_1}}} \cdot {2^{{x_2}}} = m + 2 \Leftrightarrow {2^{{x_1} + {x_2}}} = m + 2 \Leftrightarrow {x_1} + {x_2} = {\rm{lo}}{{\rm{g}}_2}\left( {m + 2} \right)\). Chọn D.
Câu hỏi cùng đoạn
Câu 2:
Số giá trị nguyên của tham số m để phương trình có hai nghiệm phân biệt thuộc khoảng\(\left( {0;2} \right)\) là:
Giải bởi Vietjack
Đặt \(t = {2^x}\,\,\left( {do\,\,0 < x < 2 \Rightarrow 1 < t < 4} \right)\), phương trình đã cho trở thành:
\({t^2} - 2mt + m + 2 = 0 \Leftrightarrow m\left( {1 - 2t} \right) = - {t^2} - 2\)\( \Leftrightarrow m = \frac{{{t^2} + 2}}{{2t - 1}}\) (*) (với \(t \in \left( {1;4} \right)\)).
Xét hàm số \(f\left( t \right) = \frac{{{t^2} + 2}}{{2t - 1}}\) với \(t \in \left( {1;4} \right)\) ta có \(f'\left( t \right) = \frac{{2t \cdot \left( {2t - 1} \right) - 2\left( {{t^2} + 2} \right)}}{{{{\left( {2t - 1} \right)}^2}}} = \frac{{2{t^2} - 2t - 4}}{{{{\left( {2t - 1} \right)}^2}}}\).
Giải \(f'\left( t \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{t = - 1\,\,\left( {ktm} \right)}\\{t = 2{\rm{\;}}\,\,\left( {tm} \right)}\end{array}} \right.\).
Ta có bảng biến thiên của hàm số \(f\left( t \right)\):
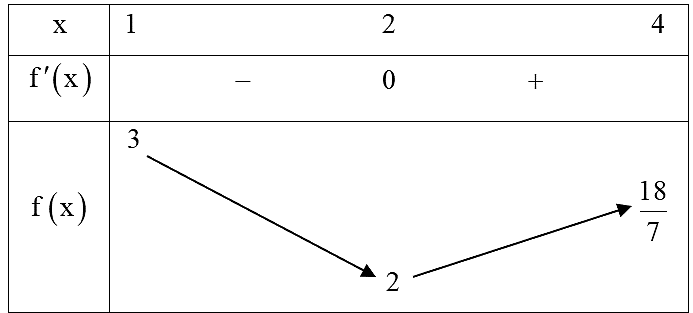
Phương trình đã cho có 2 nghiệm phân biệt thuộc khoảng \(\left( {0;2} \right)\)\( \Leftrightarrow \) phương trình (*) có 2 nghiệm phân biệt thuộc khoảng \(\left( {1;4} \right) \Leftrightarrow 2 < m < \frac{{18}}{7}\).
Do m nguyên nên không có giá trị m nào thỏa mãn. Chọn A.
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Gọi biến cố X: “Phác đồ A chữa khỏi bệnh” và biến cố Y: “Phác đồ A gây tác dụng phụ nghiêm trọng”. Ta có \(P\left( X \right) = 0,6\) và \(P\left( Y \right) = 0,05\).
Gọi biến cố M: “Phác đồ B chữa khỏi bệnh” và biến cố N: “phác đồ B gây tác dụng phụ nghiêm trọng”. Ta có \(P\left( M \right) = 0,7\) và \(P\left( N \right) = 0,1\).
Xác suất sử dụng phác đồ A gây tác dụng phụ nghiêm trọng là \(P\left( Y \right) = 0,05\) và xác suất để chọn được phác đồ A là \(P\left( A \right) = 0,5\) nên xác suất chọn được phác đồ A và bệnh nhân bị tác dụng phụ nghiêm trọng là \(0,5 \cdot 0,05 = 0,025\).
Xác suất sử dụng phác đồ B gây tác dụng phụ nghiêm trọng là \(P\left( N \right) = 0,1\) và xác suất để chọn được phác đồ B là \(P\left( B \right) = 0,5\) nên xác suất chọn được phác đồ B và bệnh nhân bị tác dụng phụ nghiêm trọng là \(0,5 \cdot 0,1 = 0,05\).
Gọi biến C: “Bệnh nhân gặp tác dụng phụ nghiêm trọng” thì \(P\left( C \right) = 0,025 + 0,05 = 0,075\).
Chọn B.
Câu 2
Lời giải
Gọi D là biến cố “bệnh nhân được chữa khỏi bệnh”.
Suy ra \(P\left( D \right) = \frac{1}{2}\left( {P\left( X \right) + P\left( M \right)} \right) = 0,65\).
Gọi \(E\) là biến cố “bệnh nhân không bị tác dụng phụ nghiêm trọng”.
Suy ra \(P\left( E \right) = \frac{1}{2}\left( {P\left( {\overline Y } \right) + P\left( {\overline N } \right)} \right)\)\( = \frac{1}{2}\left( {0,95 + 0,9} \right) = 0,925\).
Vậy xác suất để bệnh nhân chữa khỏi bệnh và không bị tác dụng phụ nghiêm trọng là:
\(P\left( {D \cap E} \right) = P\left( D \right) \cdot P\left( E \right) = 0,60125\). Chọn D.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập