Câu hỏi:
26/04/2025 11
Dựa vào thông tin dưới đây để trả lời các câu từ 76 đến 77
Cho phương trình \(\log _3^2x + \sqrt {\log _3^2x + 1} - 2m - 1 = 0\), với m là tham số thực.
Phương trình đã cho có ít nhất một nghiệm thuộc đoạn \(\left[ {1\,;\,{3^{\sqrt 3 }}} \right]\) khi và chỉ khi
Dựa vào thông tin dưới đây để trả lời các câu từ 76 đến 77
Cho phương trình \(\log _3^2x + \sqrt {\log _3^2x + 1} - 2m - 1 = 0\), với m là tham số thực.
Phương trình đã cho có ít nhất một nghiệm thuộc đoạn \(\left[ {1\,;\,{3^{\sqrt 3 }}} \right]\) khi và chỉ khi
Đáp án chính xác
Quảng cáo
Trả lời:
Giải bởi Vietjack
Từ điều kiện: \(x \in \left[ {1\,;\,{3^{\sqrt 3 }}} \right] \Leftrightarrow 1 \le x \le {3^{\sqrt 3 }} \Leftrightarrow 0 \le {\log _3}x \le \sqrt 3 \)
\( \Leftrightarrow 1 \le \log _3^2x + 1 \le 4\)\( \Leftrightarrow 1 \le \sqrt {\log _3^2x + 1} \le 2 \Leftrightarrow 1 \le t \le 2\).
Cách 1: Phương trình đã cho có ít nhất một nghiệm thuộc đoạn \(\left[ {1\,;\,{3^{\sqrt 3 }}} \right]\)
\( \Leftrightarrow \) phương trình \(f\left( t \right) = {t^2} + t - 2m - 2 = 0\) có ít nhất một nghiệm thuộc đoạn \(\left[ {1\,;\,2} \right]\)
\( \Leftrightarrow \) đường thẳng \(y = 2m + 2\) cắt phần đồ thị hàm số \(y = {t^2} + t\) lấy trên đoạn \(\left[ {1\,;\,2} \right]\) tại ít nhất một điểm.
Ta xét hàm số \(y = {t^2} + t\).
+) Miền xác định \(D = \left[ {1\,;\,2} \right]\).
+) Đạo hàm \(y' = 2t + 1,\,\,y' = 0 \Leftrightarrow 2t + 1 = 0 \Leftrightarrow t = - \frac{1}{2}\).
+) Bảng biến thiên:
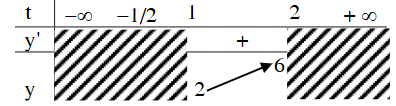
Vậy điều kiện là: \(2 \le 2m + 2 \le 6 \Leftrightarrow 0 \le m \le 2\).
Cách 2: Phương trình đã cho có ít nhất một nghiệm thuộc đoạn \(\left[ {1\,;\,{3^{\sqrt 3 }}} \right]\)
\( \Leftrightarrow \) phương trình \(f\left( t \right) = {t^2} + t - 2m - 2 = 0\) có ít nhất một nghiệm thuộc đoạn \(\left[ {1\,;\,2} \right]\)
\( \Leftrightarrow \) đường thẳng \(y = 2m + 2\) cắt phần đồ thị hàm số \(y = {t^2} + t\) lấy trên đoạn \(\left[ {1\,;\,2} \right]\) tại ít nhất một điểm.
Ta xét hàm số \(y = {t^2} + t\).
+) Miền xác định \(D = \left[ {1\,;\,2} \right]\).
+) Đạo hàm \(y' = 2t + 1 > 0,\,\forall t \in D\). Suy ra hàm số đồng biến trên \(D\).
Vậy điều kiện là: \(y\left( 1 \right) \le 2m + 2 \le y\left( 2 \right) \Leftrightarrow 2 \le 2m + 2 \le 6 \Leftrightarrow 0 \le m \le 2\).
Cách 3: Phương trình đã cho có ít nhất một nghiệm thuộc đoạn \(\left[ {1\,;\,{3^{\sqrt 3 }}} \right]\)
\( \Leftrightarrow \) phương trình \(f\left( t \right) = {t^2} + t - 2m - 2 = 0\) có ít nhất một nghiệm thuộc đoạn \(\left[ {1\,;\,2} \right]\)
\( \Leftrightarrow \) phương trình \(f\left( t \right) = {t^2} + t - 2m - 2 = 0\) có nghiệm thỏa mãn:
\(\left[ \begin{array}{l}1 < {t_1} \le {t_2} < 2\\{t_1} \le 1 \le {t_2} \le 2\\1 \le {t_1} \le 2 \le {t_2}\end{array} \right.\) với \({t_1} + {t_2} = - 1\) \( \Leftrightarrow f\left( 1 \right) \cdot f\left( 2 \right) \le 0 \Leftrightarrow - 2m\left( {4 - 2m} \right) \le 0 \Leftrightarrow 0 \le m \le 2\). Chọn D.
Nhà sách vietjack
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 3:
Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào trong các khoảng dưới đây?
Xem đáp án »
26/04/2025
42
Câu 5:
Góc giữa hai vectơ \(\overrightarrow {A'H} ,\,\,\overrightarrow {AH} \) bằng
Xem đáp án »
26/04/2025
34
🔥 Đề thi HOT:
-
Đề thi Đánh giá năng lực ĐHQG Hồ Chí Minh năm 2025 có đáp án (Đề 1)
-
(2025) Đề thi thử Đánh giá năng lực ĐHQG Hồ Chí Minh năm 2025 có đáp án (Đề 1)
-
ĐGNL ĐHQG TP.HCM - Sử dụng ngôn ngữ Tiếng Việt - Chính tả
-
Đề thi Đánh giá năng lực ĐHQG Hồ Chí Minh năm 2025 có đáp án (Đề 2)
-
Đề thi Đánh giá năng lực ĐHQG Hồ Chí Minh năm 2025 có đáp án (Đề 3)
-
(2025) Đề thi thử Đánh giá năng lực ĐHQG Hồ Chí Minh năm 2025 có đáp án (Đề 2)
-
(2025) Đề minh họa Đánh giá năng lực ĐHQG Hồ Chí Minh năm 2025 có đáp án ( Đề 8)
-
Đề thi Đánh giá năng lực ĐHQG Hồ Chí Minh năm 2025 có đáp án (Đề 4)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận