Dựa vào thông tin dưới đây để trả lời các câu từ 85 đến 87
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy là tam giác đều cạnh \(2a,\,\,AA' = a\sqrt 3 \). Gọi \(H,\,\,K\) lần lượt là trung điểm \(BC,\,\,B'C'\).
Góc giữa hai vectơ \(\overrightarrow {A'H} ,\,\,\overrightarrow {AH} \) bằng
Dựa vào thông tin dưới đây để trả lời các câu từ 85 đến 87
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy là tam giác đều cạnh \(2a,\,\,AA' = a\sqrt 3 \). Gọi \(H,\,\,K\) lần lượt là trung điểm \(BC,\,\,B'C'\).
Câu hỏi trong đề: Đề thi ĐGNL ĐHQG Hồ Chí Minh (V-ACT) năm 2026-2027 (Đề 21) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
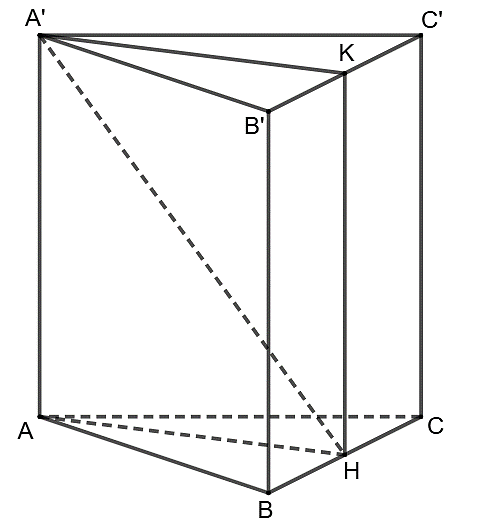
Ta có \(AH = \frac{{AB\sqrt 3 }}{2} = \frac{{2a\sqrt 3 }}{2} = a\sqrt 3 \). Khi đó, hình chữ nhật \(AA'KH\) có \(AH = AA' = a\sqrt 3 \) nên \(AA'KH\) là hình vuông. Suy ra \(\widehat {HA'K} = 45^\circ \).
Ta có \(\left( {\overrightarrow {A'H} ,\,\,\overrightarrow {AH} } \right) = \left( {\overrightarrow {A'H} ,\,\,\overrightarrow {A'K} } \right) = \widehat {HA'K} = 45^\circ \). Chọn B.
Câu hỏi cùng đoạn
Câu 2:
Độ dài của vectơ \(\overrightarrow {AK} + \overrightarrow {AH} \) là:
Giải bởi Vietjack
Gọi I là trung điểm HK, suy ra \({\rm{IH}} = \frac{{a\sqrt 3 }}{2}\).
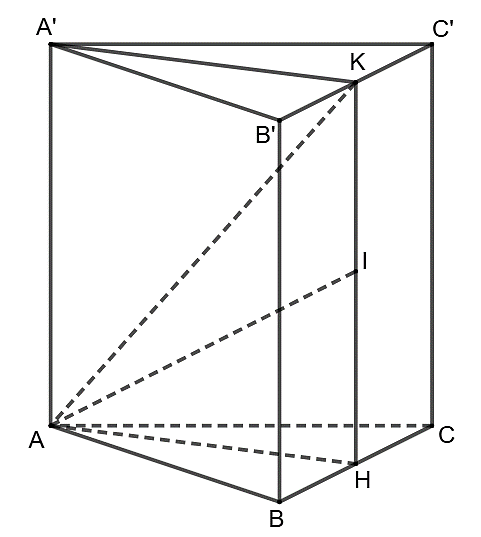
Khi đó, \(AI = \sqrt {I{H^2} + A{H^2}} = \frac{{a\sqrt {15} }}{2}\). Ta có\(\left| {\overrightarrow {AK} + \overrightarrow {AH} } \right| = \left| {2\overrightarrow {AI} } \right| = 2AI = a\sqrt {15} \). Chọn A.
Câu 3:
Tích vô hướng của hai vectơ \(\overrightarrow {AK} \) và \(\overrightarrow {AB'} \) bằng
Giải bởi Vietjack
Ta có \(AB' = AC' = a\sqrt 7 \) nên tam giác \({\rm{AB'C'}}\) cân tại A, suy ra AK vuông góc \({\rm{B'C'}}\).
Ta có \({\rm{AK}}\,{\rm{ = }}\,\sqrt {A{H^2} + K{H^2}} = a\sqrt 6 ;\,\,{\rm{B'K}}\,{\rm{ = }}\frac{{B'C'}}{2} = \frac{{2a}}{2} = {\rm{a}}\).
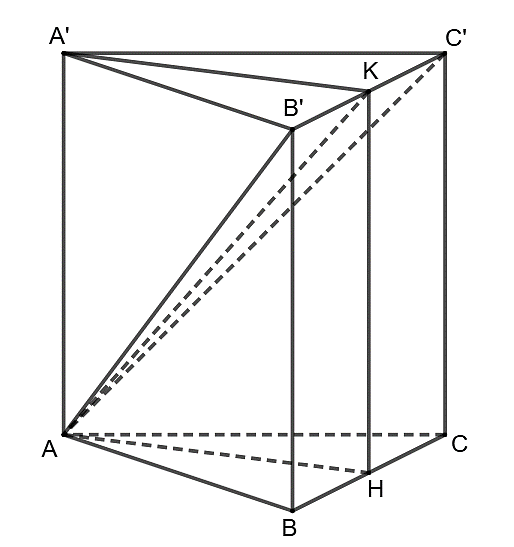
Xét tam giác \(AKB'\) có cos \(\cos \widehat {KAB'} = \frac{{AK}}{{AB'}} = \frac{{a\sqrt 6 }}{{a\sqrt 7 }} = \sqrt {\frac{6}{7}} \).
Khi đó, \(\overrightarrow {AK} \cdot \overrightarrow {AB'} = \left| {\overrightarrow {AK} } \right| \cdot \left| {\overrightarrow {AB'} } \right| \cdot {\rm{cos}}\left( {\overrightarrow {AK} ,\overrightarrow {AB'} } \right) = AK \cdot AB' \cdot {\rm{cos}}\widehat {KAB'} = 6{a^2}\). Chọn A.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Ta có \(\mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {{x^2} + 2x + 2} }}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {1 + \frac{2}{x} + \frac{2}{{{x^2}}}} }}{1} = 1\).
\[\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} + 2x + 2} - x} \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{2x + 2}}{{\sqrt {{x^2} + 2x + 2} + x}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{2 + \frac{2}{x}}}{{\sqrt {1 + \frac{2}{x} + \frac{2}{{{x^2}}}} + 1}} = 1\].
Ta có \(\mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {{x^2} + 2x + 2} }}{x} = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - \sqrt {1 + \frac{2}{x} + \frac{2}{{{x^2}}}} }}{1} = - 1\).
\[\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} + 2x + 2} + x} \right) = \mathop {\lim }\limits_{x \to - \infty } \frac{{2x + 2}}{{\sqrt {{x^2} + 2x + 2} - x}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{2 + \frac{2}{x}}}{{ - \sqrt {1 + \frac{2}{x} + \frac{2}{{{x^2}}}} - 1}} = - 1\].
Vậy đồ thị hàm số có hai tiệm cận xiên là: \(y = x + 1\) và \(y = - x - 1\). Chọn C.
Câu 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Ta có \(h\left( t \right)\) là một nguyên hàm của hàm số \(v\left( t \right) = - 0,1{t^3} + 1,1{t^2}\) nên
\(h\left( t \right) = \int {v\left( t \right)dt} = \int {\left( { - 0,1{t^3} + 1,1{t^2}} \right)dt} = - \frac{1}{{40}}{t^4} + \frac{{11}}{{30}}{t^3} + C\).
Do \(h\left( 0 \right) = 20\) nên \(C = 20\). Vậy \(h\left( t \right) = - \frac{1}{{40}}{t^4} + \frac{{11}}{{30}}{t^3} + 20\). Chọn A.
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(a = - 1;b = 0\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập